摘要：Split Sum通过将环境光照积分拆分为BRDF滤波和光照滤波两部分，利用预计算降维技术加速实时渲染。BRDF部分采用菲涅尔近似降维，光照部分使用多级mipmap快速查询，显著提升PBS的IBL计算效率。

基于图像的光照(Image based lighting, IBL)是一类光照技术的集合.其光源不是如点光源等直接光源,而是将周围环境整体视为一个大光源.

那么在shader中我们有了一张cubeMap(也可能是别的形式),如何用它来实现PBS(Physically Based Shading)呢?

或者说,我们如何用一张环境贴图来解渲染方程呢?

首先回顾渲染方程:

L(p,ωo)=∫H2f(p,ωi⋅ωo)Li(p,ωi)V(p,wi)cos⁡θidwiL(p, \omega_o) = \int_{H^2} f(p, \omega_i \cdot \omega_o) L_i(p, \omega_i) V(p,wi) \cos \theta_i dw_i

在环境光照中,我们不考虑Visibility即不考虑阴影(任何方向光照都能到达),所以可以去除这一项:

L(p,ωo)=∫H2f(p,ωi⋅ωo)Li(p,ωi)cos⁡θidwiL(p, \omega_o) = \int_{H^2} f(p, \omega_i \cdot \omega_o) L_i(p, \omega_i) \cos \theta_i dw_i

我们可以用蒙特卡洛方法来积分:

L(p,ωo)≈1N∑i=1Nf(p,ωi⋅ωo)Li(p,ωi)cos⁡θiL(p, \omega_o) \approx \frac{1}{N} \sum_{i=1}^N f(p, \omega_i \cdot \omega_o) L_i(p, \omega_i) \cos \theta_i

但是问题是蒙特卡洛积分需要大量的采样,如果在shader里用的话,速度肯定会十分感人.
那么如何去避免采样来计算呢?

人们观察到一件事情:

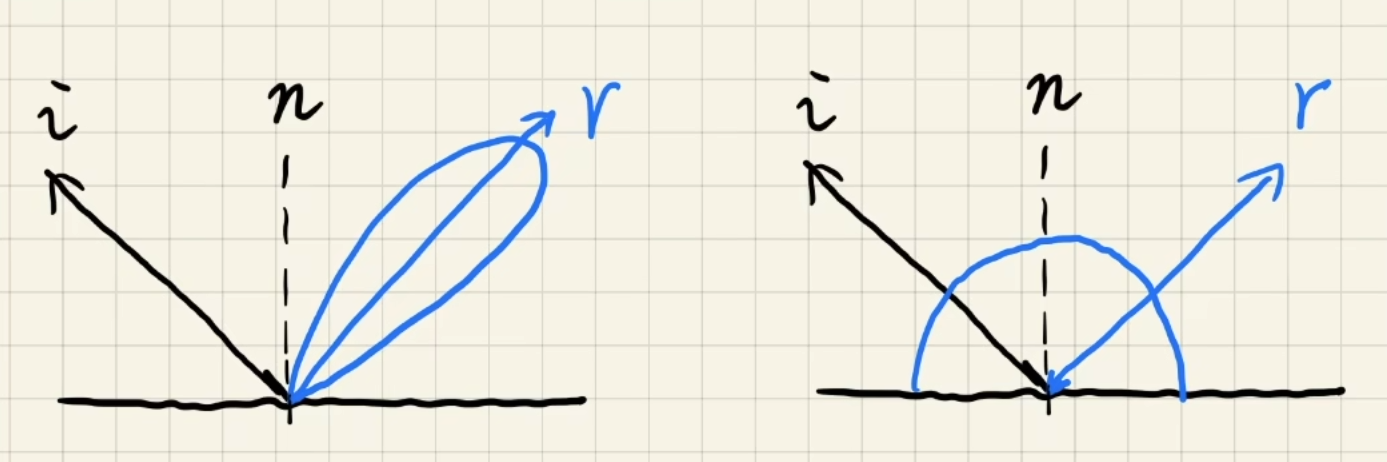
  • 如果BRDF比较glossy,虽然值变化大,但是"积分域"小
  • 如果BRDF比较diffuse,虽然"积分域"大,但是值变化小.
BRDF

如果读者阅读过这篇文章,马上就会想起这个约等式:

∫Ωf(x)g(x)dx≈∫ΩGf(x)dx∫ΩGdx∫Ωg(x)dx\int_{\Omega} f(x) g(x) dx \approx \frac{\int_{\Omega_G} f(x) dx}{\int_{\Omega_G} dx} \int_{\Omega} g(x) dx

注意这里有一点小区别:f(x)f(x)的积分域变成了整个范围中g(x)g(x)有值的地方.

而这个约等式在以下情况比较准确:

  • "积分域"小
  • 值变化小

那BRDF不是正好很满足这个性质吗?

那么我们可以更改我们的渲染方程:

L(p,ωo)≈∫ΩfrLi(p,ωi)dwi∫Ωfrdwi∫Ωfr(p,ωi⋅ωo)cos⁡θidwiL(p, \omega_o) \approx \frac{\int_{\Omega_{fr}} L_i(p, \omega_i) dw_i}{\int_{\Omega_{fr}} dw_i} \int_{\Omega} f_r(p, \omega_i \cdot \omega_o) \cos \theta_i dw_i

相当于把BRDF的lobe上的Li积分起来然后normalize.
不就是filting吗?而filter就是lobe的大小.
filtinig in different lobes

更详细地说,看下图:

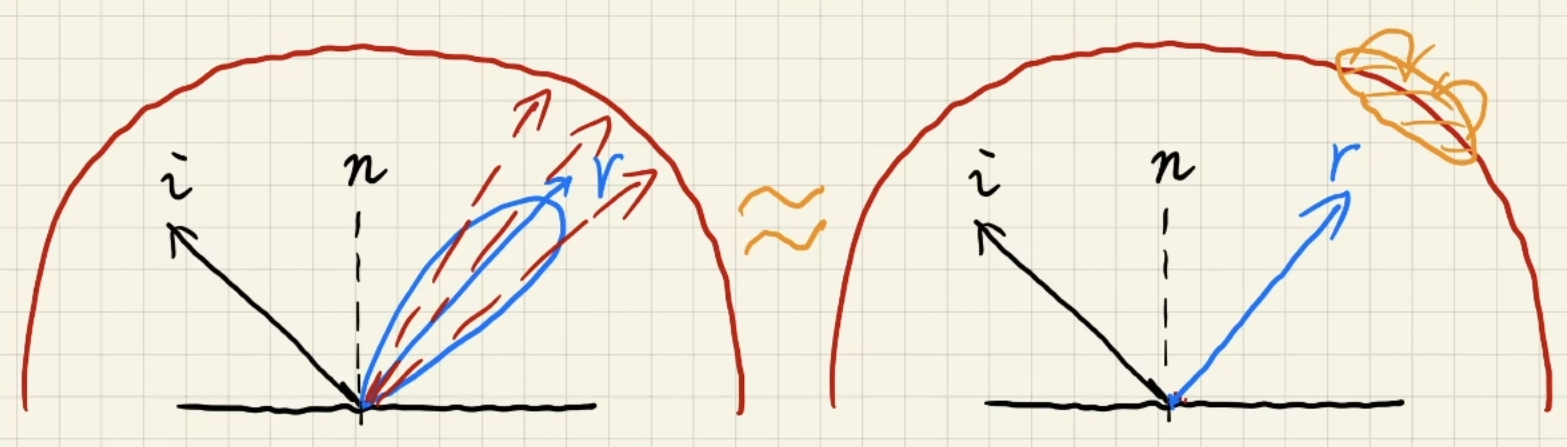
左边是正确的做法:在lobe里采样多次没有滤波的环境贴图.
就相当于采样一次镜面反射方向已经根据lobe大小进行滤波的环境贴图.

那么我们只要存储多张不同滤波的环境贴图,然后shading根据lobe大小选择对应的贴图进行三线性插值,就可以快速计算∫ΩfrLi(p,ωi)dwi∫Ωfrdwi\frac{\int_{\Omega_{fr}} L_i(p, \omega_i) dw_i}{\int_{\Omega_{fr}} dw_i}

但是∫Ωfr(p,ωi⋅ωo)cos⁡θidwi\int_{\Omega} f_r(p, \omega_i \cdot \omega_o) \cos \theta_i dw_i要如何进行积分呢?

我们可以想到使用预计算的方法,把所有可能的情况计算出来并且存储起来,但是问题也显然:
我们需要一个五维的表格来存储,这显然会占用太大内存.

那么如何降低这个维度呢?

如果回看Cook-Torrance BRDF,事实上我们只需要3个参数:

  • 入射角θi\theta_i
  • F0F_0
  • roughnessroughness

三维似乎已经可以接受了,但是大佬又搞出来骚方法把三维降成了2维.怎么做到的呢?

首先起源于一个对菲涅尔项(使用Schlick近似)的发现:
如果我们将菲涅尔项从BRDF中提取出来可以得到:

∫Ω+fr(p,ωi,ωo)cos⁡θi dωi≈F0∫Ω+frF(1−(1−cos⁡θi)5)cos⁡θi dωi+∫Ω+frF(1−cos⁡θi)5cos⁡θi dωi\int_{\Omega^+} f_r(p, \omega_i, \omega_o) \cos \theta_i \, d\omega_i \approx F_0 \int_{\Omega^+} \frac{f_r}{F} \left( 1 - (1 - \cos \theta_i)^5 \right) \cos \theta_i \, d\omega_i + \int_{\Omega^+} \frac{f_r}{F} (1 - \cos \theta_i)^5 \cos \theta_i \, d\omega_i

这样我们可以将F0F_0从积分中提取出来,那么积分部分就只依赖两个变量(roughnessroughness和ωi\omega_i),从而达到降维了.

这样我们可以预计算一张纹理两通道的纹理,r通道记录第一个积分,g通道记录第二个积分,这样计算时只需要查询两次就可以解决了.
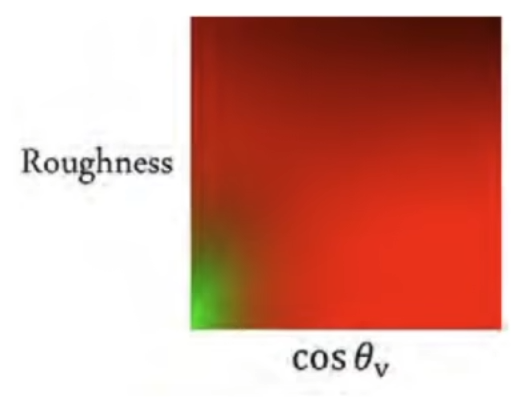
split sum

这样,通过两种不同处理,我们就完美解决了环境光照积分的问题,而且结果和效率都十分喜人.这种方法被称为Split Sum.
Split Sum

至于为什么不叫Split Integral,是因为实时渲染中一般将公式写为求和的形式而非积分的形式,即:

1N∑k=1NLi(lk)f(lk,v)cos⁡θlkp(lk,v)≈(1N∑k=1NLi(lk))(1N∑k=1Nf(lk,v)cos⁡θlkp(lk,v))\frac{1}{N} \sum_{k=1}^{N} \frac{L_i(\mathbf{l}_k) f(\mathbf{l}_k, \mathbf{v}) \cos \theta_{l_k}}{p(\mathbf{l}_k, \mathbf{v})} \approx \left( \frac{1}{N} \sum_{k=1}^{N} L_i(\mathbf{l}_k) \right) \left( \frac{1}{N} \sum_{k=1}^{N} \frac{f(\mathbf{l}_k, \mathbf{v}) \cos \theta_{l_k}}{p(\mathbf{l}_k, \mathbf{v})} \right)

那么只剩下一个问题了:有遮挡时应该怎么做呢,即怎么计算Visibility?
事实上,这件事情非常困难,到2024年为止还没有很好的解决方法.

但是有一个凑合的办法:从环境贴图中找一个最亮的光源生成shadow