PBR--从理论到实际

状态: 更新中…

---

Intro

前置知识

辐射度量学

下面的所有概念,请记英文(因为中文翻译千奇百怪).

Radiant Energy(辐射能量)

单位: J(焦耳)

用于描述能量的大小.比如一颗原子弹能释放的总能量大约为10^10 J.

Radiant Flux(辐射通量)

单位: W(瓦特)
单位: lm(流明,照明度单位,lumen)
单位: J/s(焦耳每秒)

描述单位时间内通过某一面积的辐射能量.比如太阳mitted的辐射通量大约为3.828 x 10^26 W/m^2.

Radiant Intensity(辐射强度)

功率/立体角

单位: W/sr (瓦每立体角)

单位: cd(坎德拉,candela)

太阳照的坎德拉为3.828 x 10^10 cd/m^2.
地球在太阳的立体角为: 23.45 deg.
可求太阳对输出的功率为: 3.828 x 10^10 W/m^2 * 23.45 deg = 1.05 x 10^11 W/sr.

再比如这个灯泡:

Irradiance

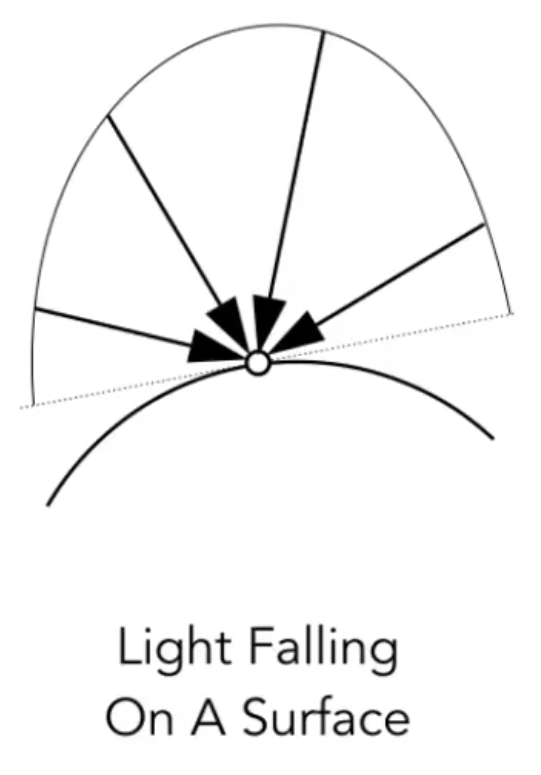
功率/面积

单位: W/m^2 (瓦每平方米)

单位: lm/m^2 (流明每平方米)

单位: lux(照度)

值得注意的是,面积必须得是垂直于光线的面积.

这一点和Lambert’s Cosine Law有关.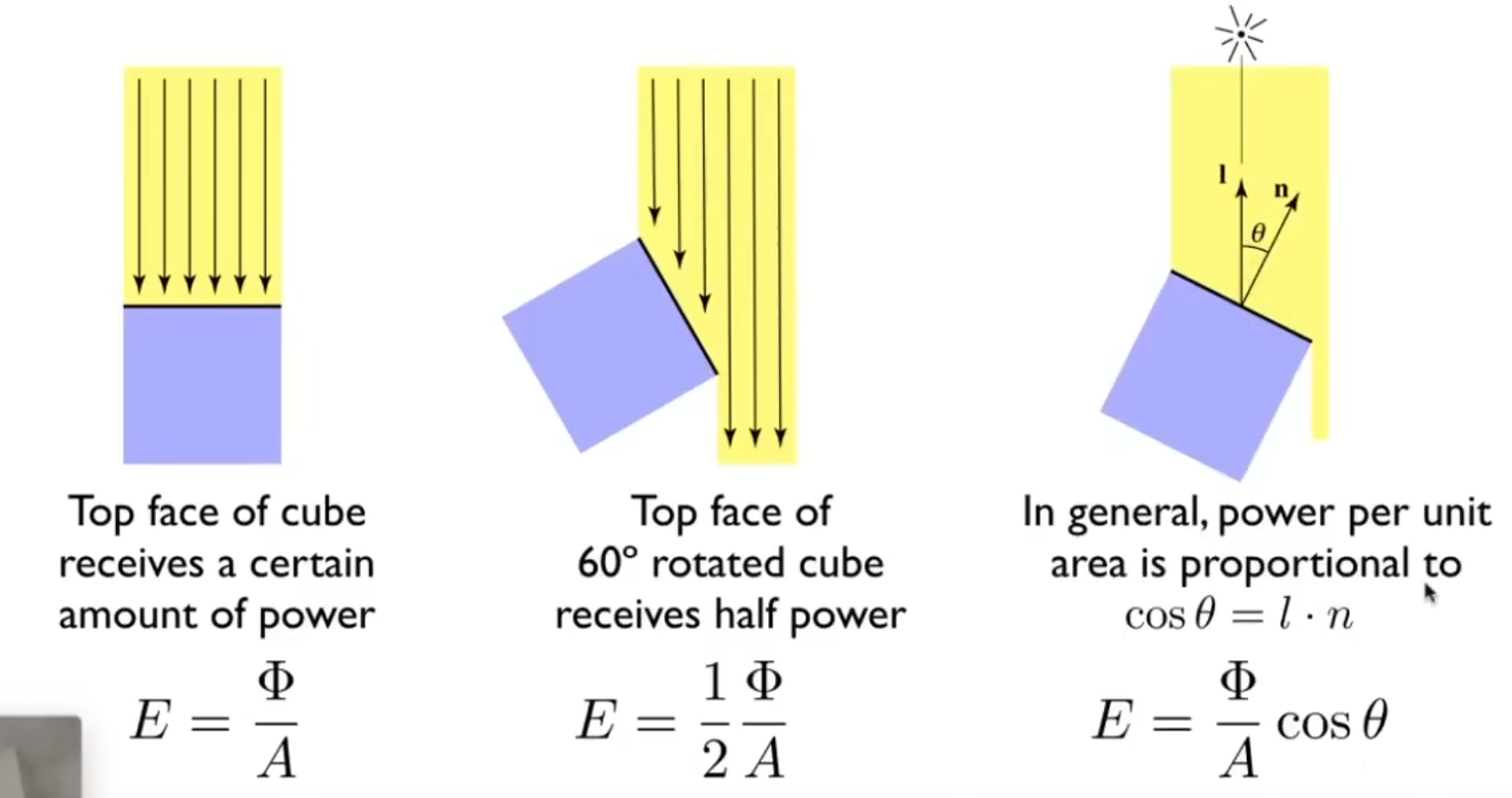

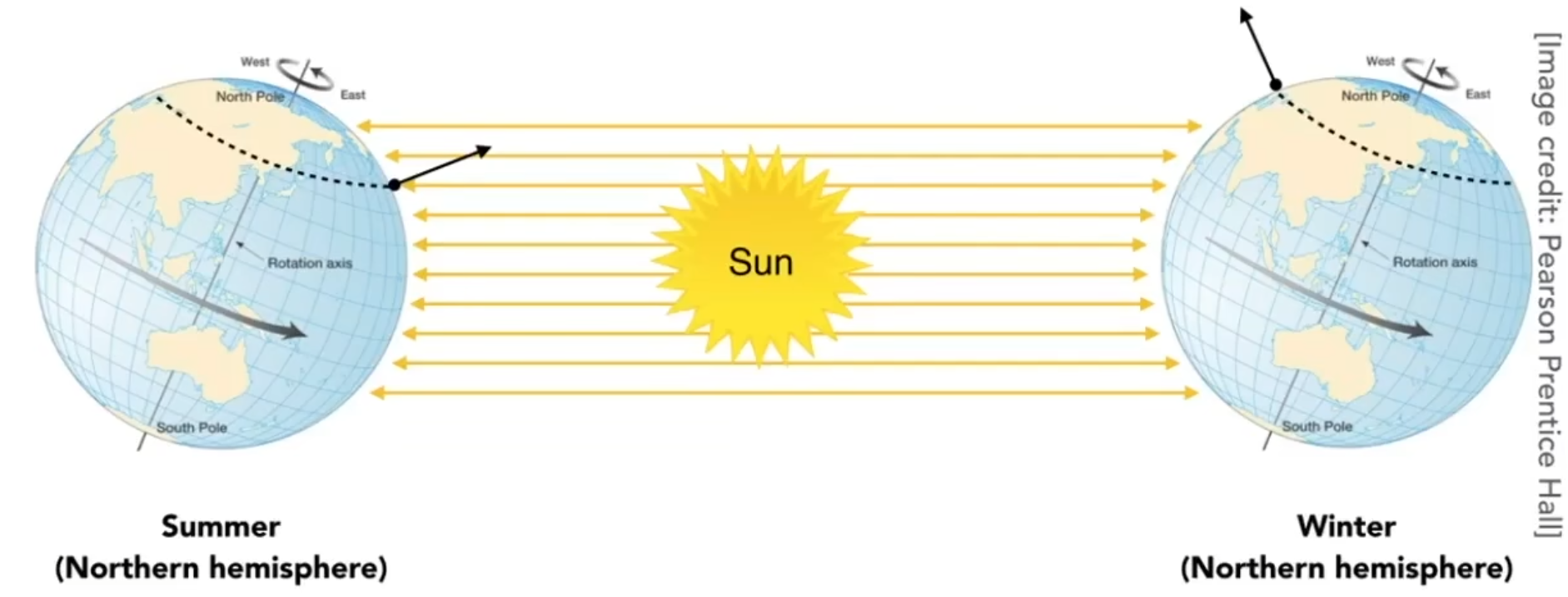
帮助理解:

• 一年四季
• Irradiance Falloff 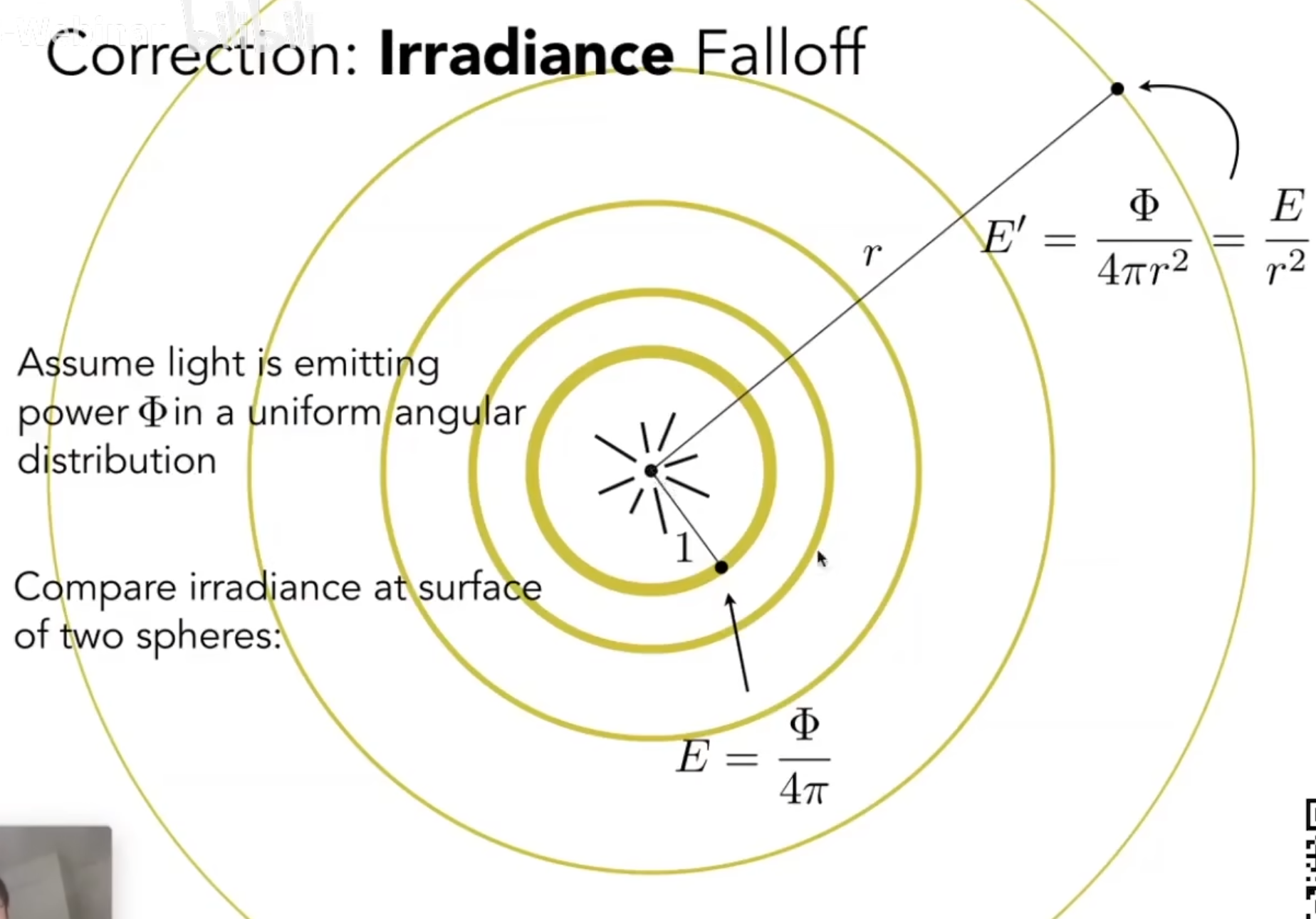单位能量不变,面积越大,能量越少. Intensity 不变,Irradiance 衰减.

Radiance

为了描述一条光线.

功率/(面积 * 立体角)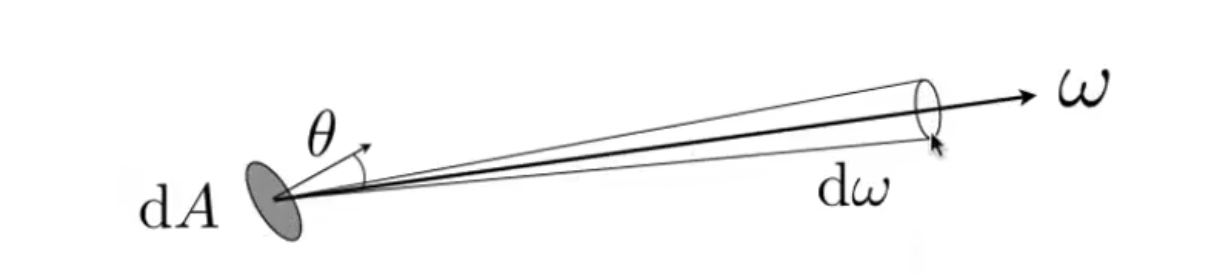

单位: W/(m^2 * sr) (瓦每平方米每立体角)

单位: cd/m^2 (坎德拉每平方米)(Exit Radiance)

单位: lux/sr (照度每立体角)(Incident Radiance)

单位: nit (尼特)

Incident Radiance(入射辐射度)

Irradiance/立体角

单位: radiance (辐射度)

单位: W/(m^2 * sr) (瓦每平方米每立体角)

单位: lux/sr (照度每立体角)

Exit Radiance(出射辐射度)

Intensity/面积

单位: radiance (辐射度)

单位: W/(m^2 * sr) (瓦每平方米每立体角)

单位: cd/m^2 (坎德拉每平方米)

Irradiance 和 Radiance

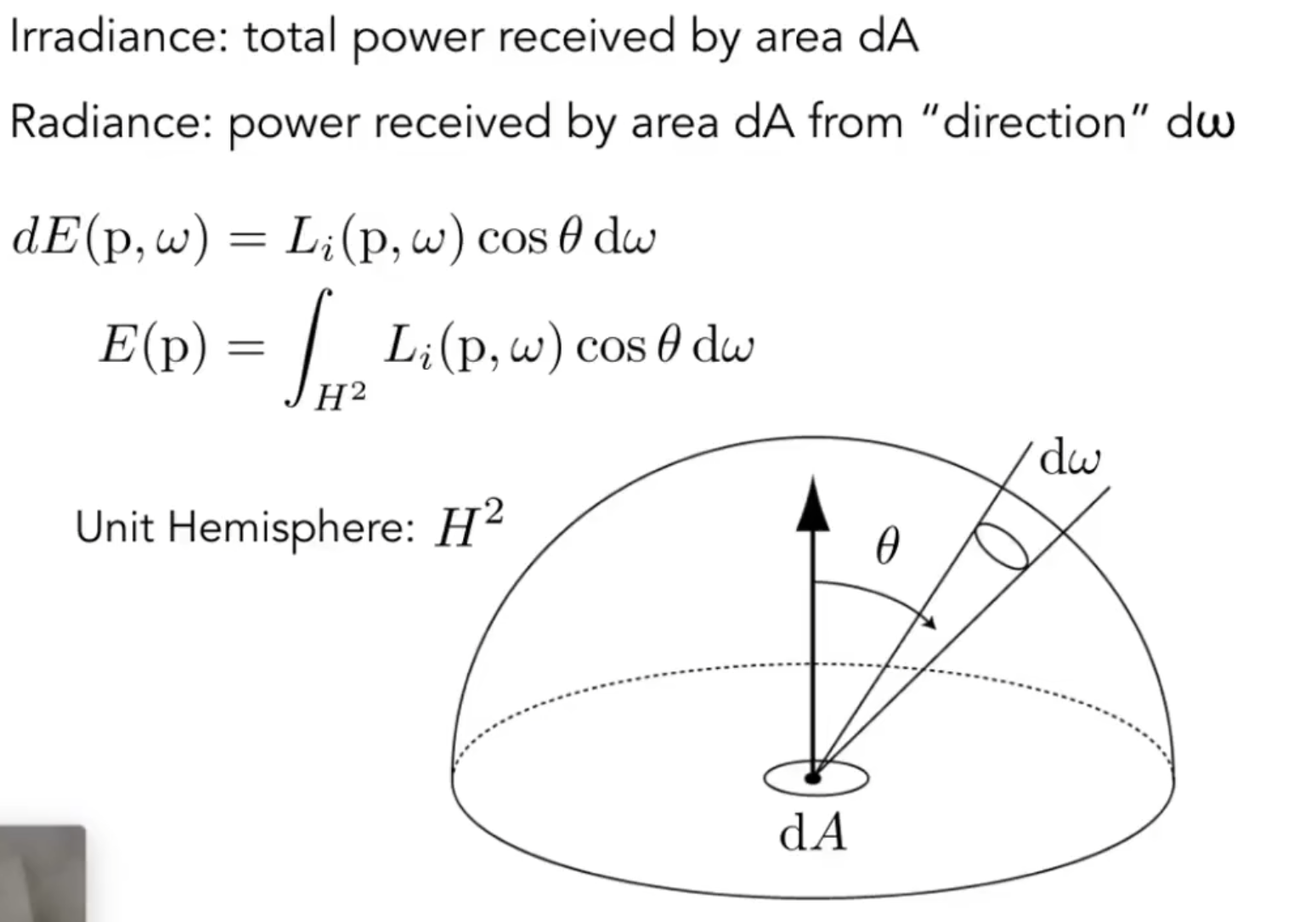
Irradiance:$dA$收到的所有能量

Radiance: 从$dw$过来的被$dA$吸收的能量

所以计算点p的能量就是: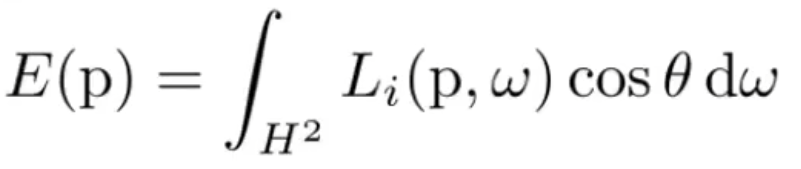

BRDF(Bidirectional Reflectance Distribution Function)

我们先把BRDF提前拉过来帮助读者检验是否了解了上文的概念.

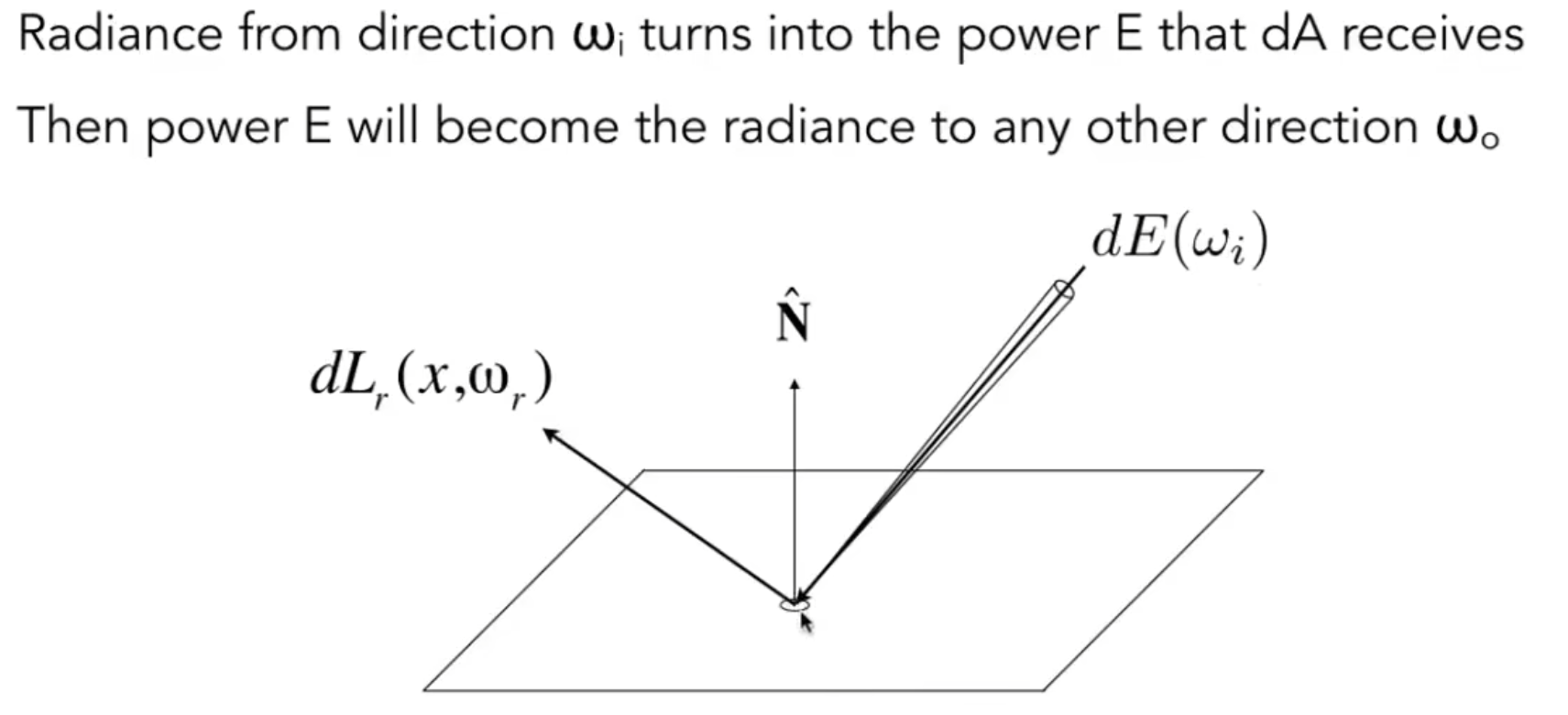
BRDF描述了从$wo$进入的Radiance反射到$wi$方向的Radiance.

或者说,BRDF描述了假设$dA$有能量,向各个方向发射光线的分布.

这个过程可以这么理解:

1. 光线从$wo$打到$dA$
2. $dA$吸收能量,有了Radiant Intensity
3. $dA$向$wi$发射光线

Render Equation

渲染方程是PBR的核心.

Reflection Equation

反射方程描述了任何一个着色点对一个出射方向发出的光线

---

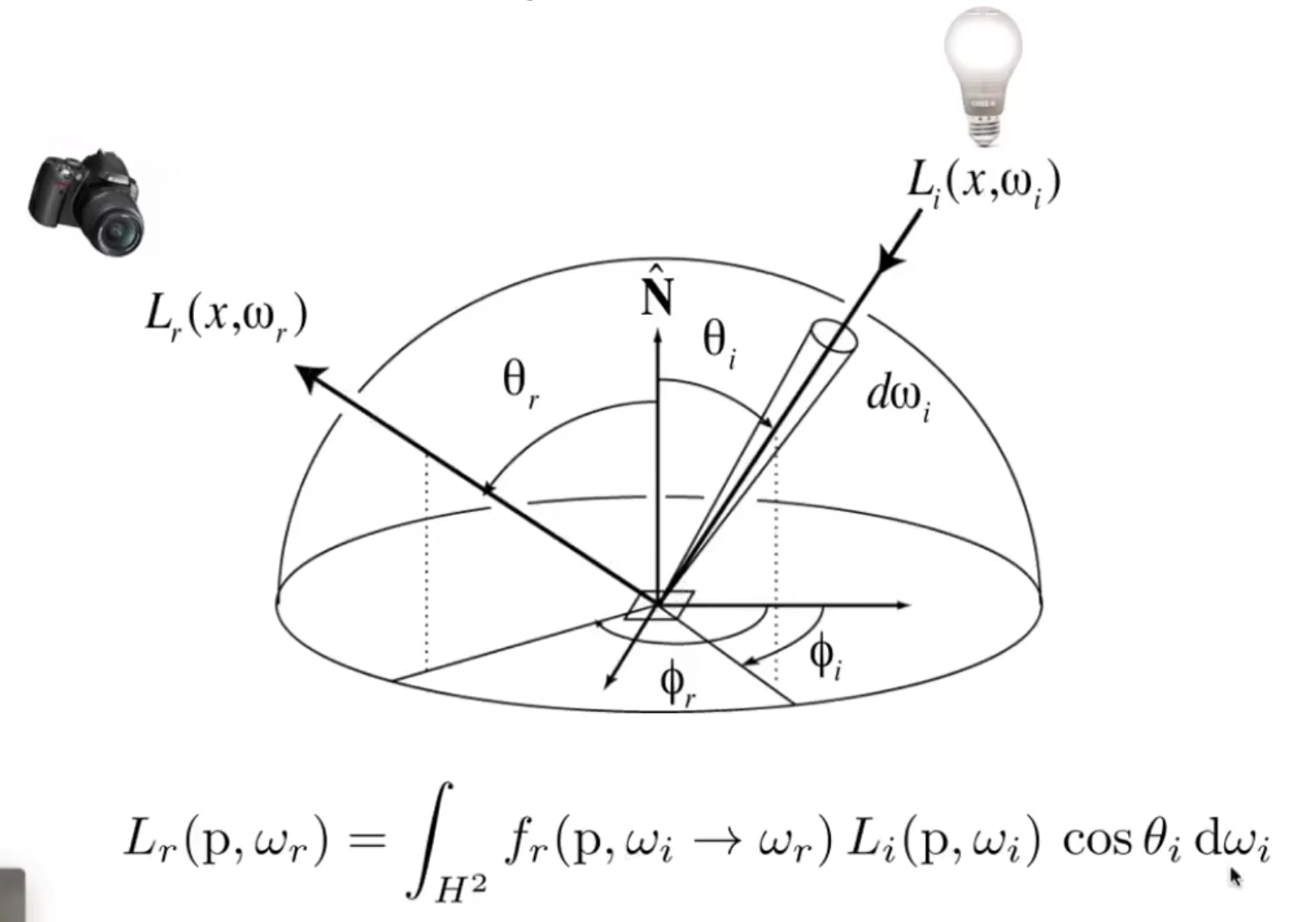
渲染方程如下:

• Le: $dA$ 本身发光
• n: 法线

渲染方程的理解

$L = E + KL$

• $L$: 光线的辐射度
• $E$: 自发光
• $K$: 反射系数
• $L$: 进入能量

$L = E + KE + K^2E + K^3E + …$

• L = 自发光 + 直接光 + 一次反射 + 二次反射 + …

材质

材质 == BxDF

BxDF各种形式分别描述了各种材质的反射行为.

• BRDF: 反射
• BTDF: 透射
• BSSRDF: 次表面散射
• BSDF: (BSDF = BRDF + BTDF)

• BRDF: Bidirectional Reflectance Distribution Function
• BTDF: Bidirectional Transmission Distribution Function
• BSSRDF: Bidirectional Surface Scattering Reflectance Distribution Function
• BSDF: Bidirectional Scattering Distribution Function

为了更好理解BxDF,我们首先需要知道光与表面的交互方式.

光与表面交互方式

讨论条件:光与光学平坦表面交互

光射到表面后会发生:

1. 反射
2. 折射

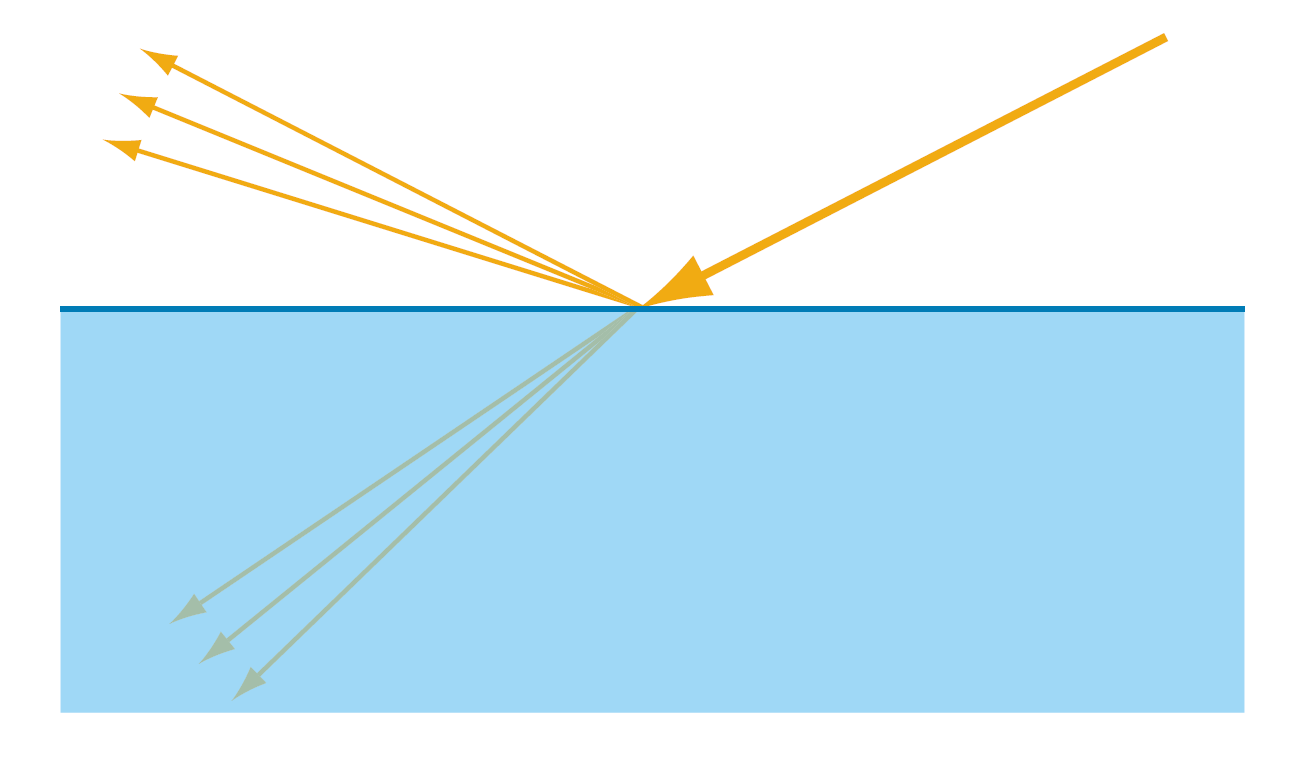
反射的光非常好理解,但是折射的光会由于对象性质有不同,简单来说:

• 对于导体,折射光会被立刻吸收,因为有自由电子接受了能量
• 对于绝缘体,折射光在其内部表现为常规的participate media(参与介质),表现出吸收与散射两种行为.

光与participate media的交互方式在后文介绍BSDF时会详细介绍.

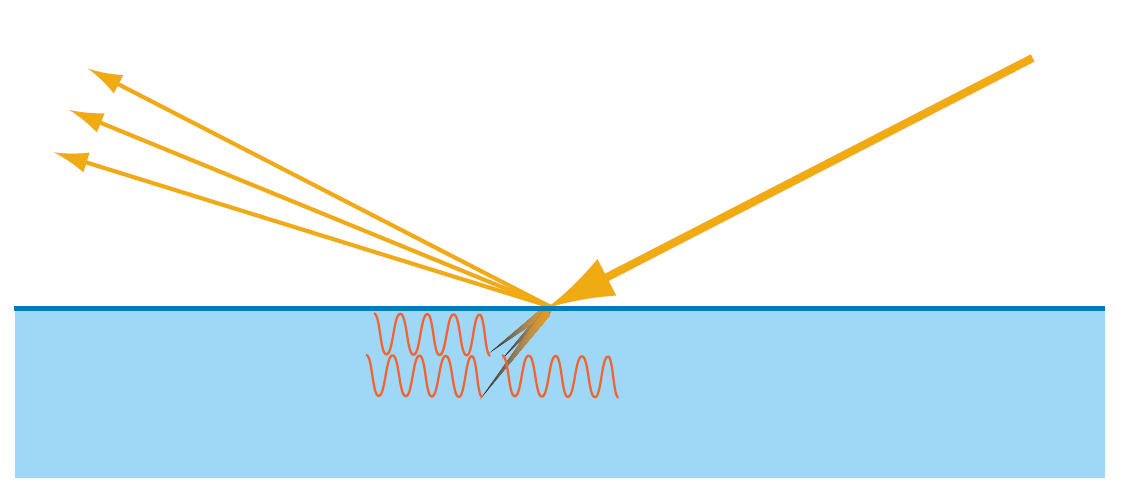
折射入非金属的光又散射出来,这种现象叫次表面散射

非金属的折射现象实际上就是所谓的漫反射

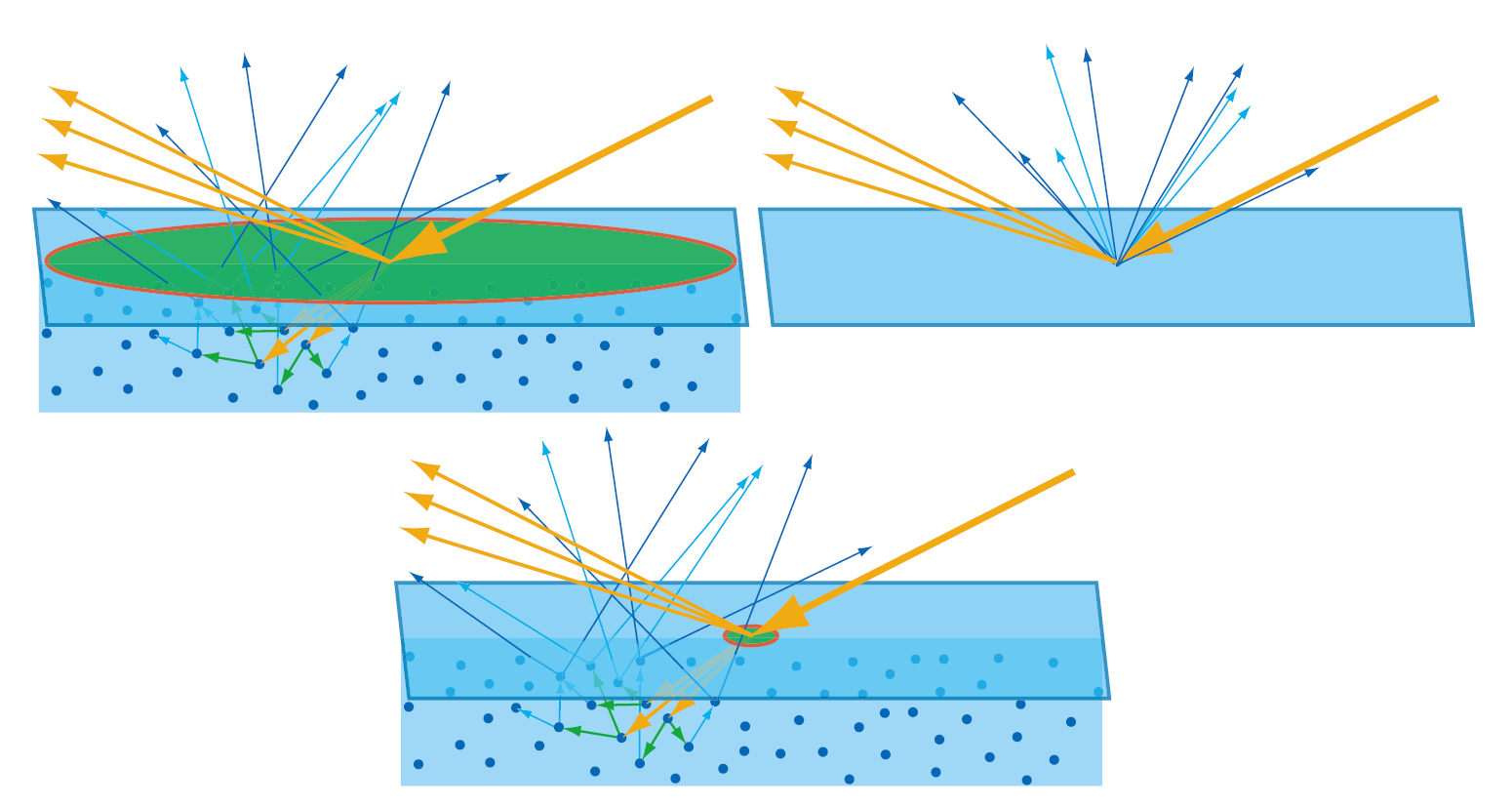
因为散射距离与像素距离相比较来说微不足道,所以我们可以将所有射出的光线认为是在光与表面的接触点射出的,这就是BRDF.而考虑了散射出表面位置已经离开了接触点的光线,这就是BSSRDF.而考虑了光线在折射后从物体的另一面离开,这就是BTDF.BSDF可以看做BRDF和BTDF更一般的形式,而且BSDF = BRDF + BTDF.

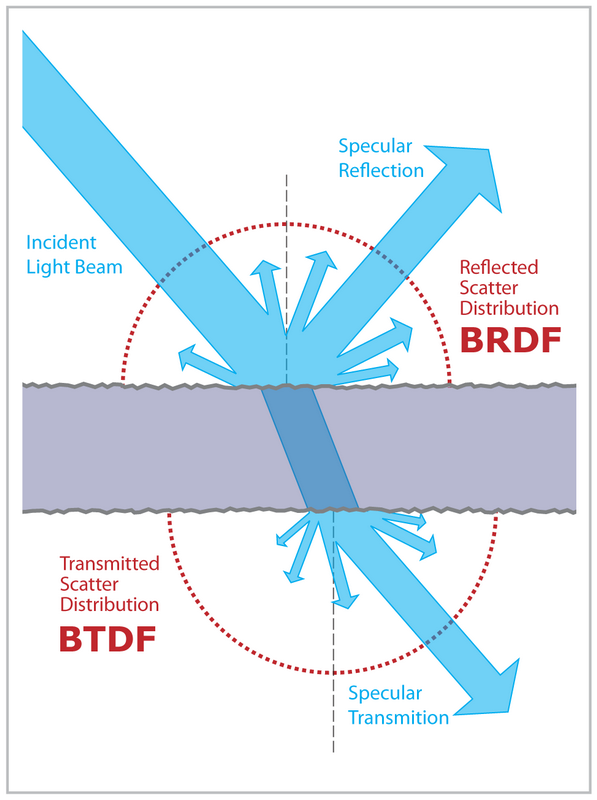
在上述这些BxDF中,BRDF最为简单,也最为常用.因为游戏和电影中的大多数物体都是不透明的,用BRDF就完全足够.而BSDF,BTDF,BSSRDF往往更多用于半透明材质和次表面散射材质.

但无论哪种BxDF,都是分为了两部分,即:直接反射部分,折射部分.

由于BRDF的性质(在后文总结),我们可以将其分为两部分:

• 直接反射部分: 直接反射光线的BRDF
• 折射部分: 折射光线的BRDF

因此可以推出公式:

$F_r = k_d f_d + k_s f_s$

其中:

• $f_d$: 漫反射部分的BRDF
• $f_s$: 折射部分的BRDF
• $k_d$: 漫反射部分占比
• $k_s$: 折射部分占比

问题来了,我怎么知道一个物体的漫反射部分占比和折射部分占比呢?
答案是菲涅尔现象,通过菲涅尔函数,我们可以计算出$k_s$
又由于能量守恒,我们可以得出: $k_d + k_s = 1$从而轻易得到$k_d$

菲涅尔现象

菲涅尔现象是指:反射会随着入射角度的变化而发生变化,尤其是当入射角度接近90度时,反射会变得很强.

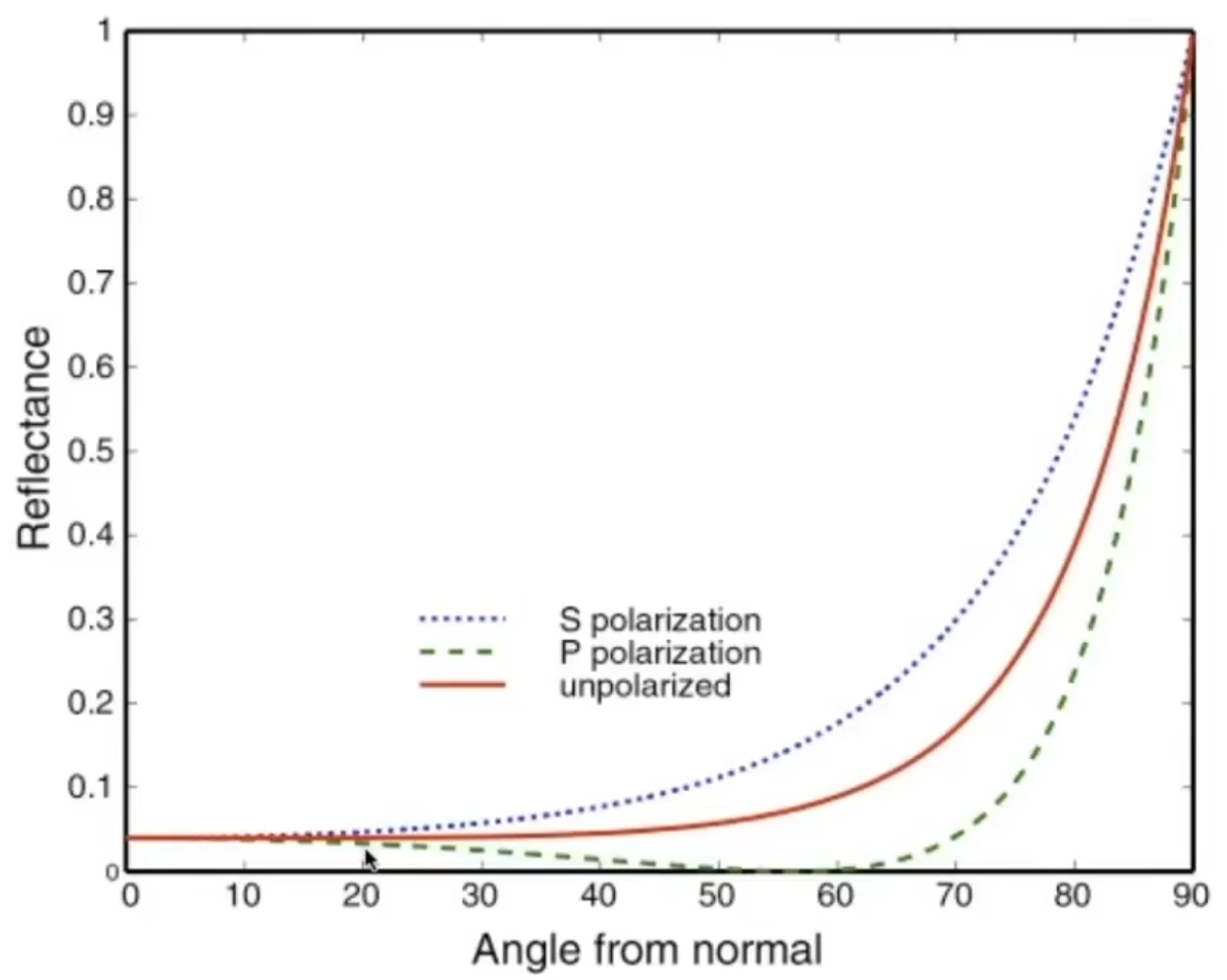
需要注意:不同的材质菲涅尔函数不相同,此函数为折射率为1.5的绝缘体的菲涅尔函数.下面这个函数则是一种导体的菲涅尔函数.

此图为不同材质的菲涅尔函数: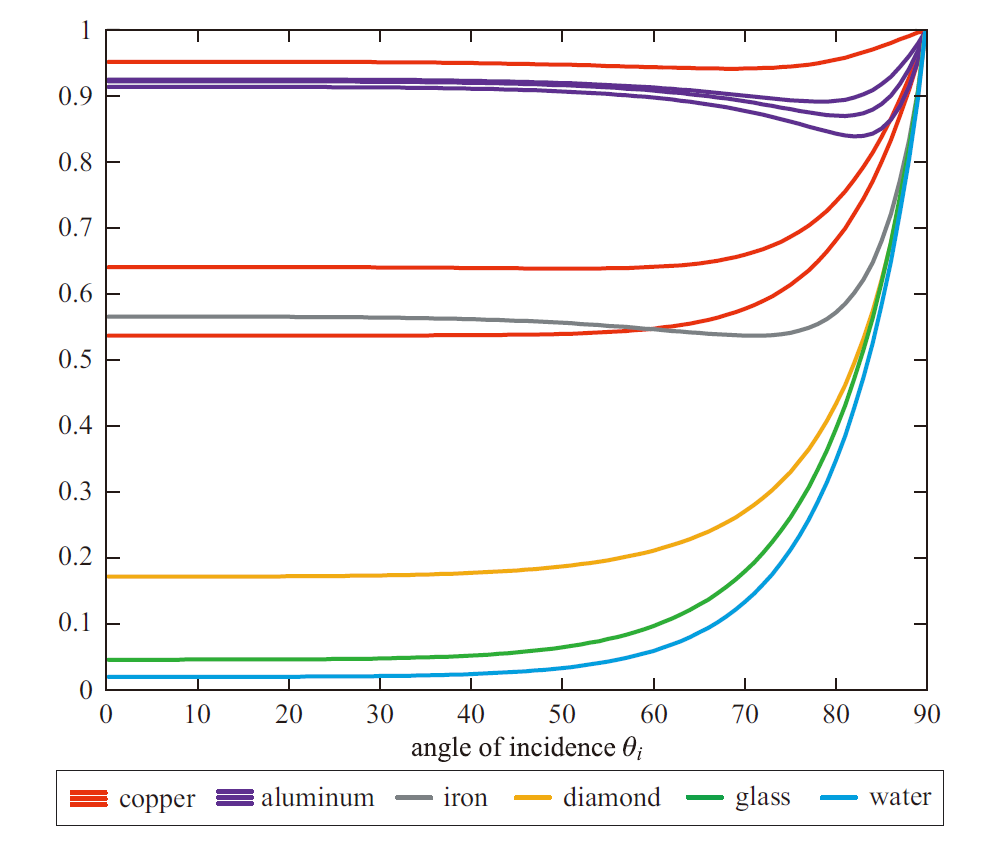

那么,菲涅尔函数如何计算呢?

在物理学上的公式如下: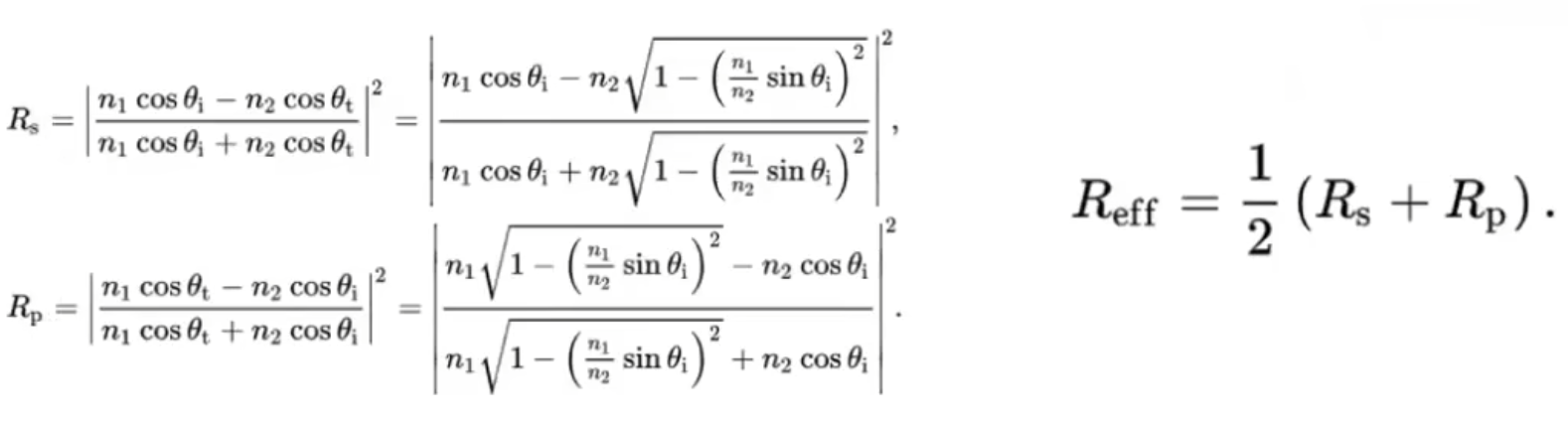

其中是s,p是光的不同极化,如果不考虑光的极化,则只需要相加/2.

可以发现,菲涅尔函数和以下参数有关:

• 入射光和法线的角度
• 材质本身性质
• 折射率变化

显然,如果在实时渲染中真使用这个公式是不可能的,图形学肯定会近似.而最常用的近似方法是使用Schlick近似.

Shchlick近似公式如下: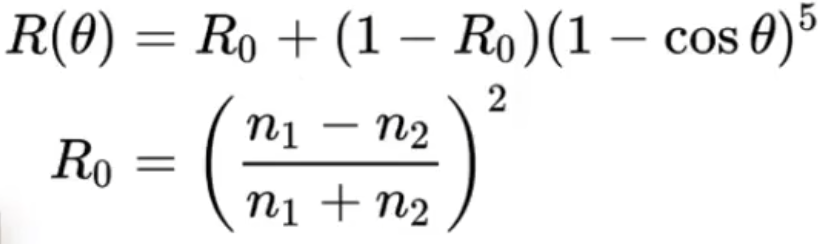

其中$n1$和$n2$是材质的折射率.

我们可以假设n1 = 1(近似于空气的折射率,除非你需要渲染的是外星异世界之类的空气折射率不为1的世界)

这样我们可以简化我们的$R_0$(下文及以后都写为$F_0$)

$F_0 = (\frac{n-1}{n+1})^2$

这样,我们就只要知道一个材质的折射率(IOR)就可以计算材质的菲涅尔项了.

下图给出了不同折射率材质效果:

但是问题在于,如果让设计师在设计材质时使用IOR,会出现很多问题:

• 范围[0,infinity]
• 非线性
• 不够直观
• etc.(具体可以看Disney PBR Principles)

不过很显然,比起调节IOR,我们可以直接调节$F_0$.最大优点在于[0,1]范围内,而且直观.

由于金属和非金属与光交互的性质不一,详见前文.导致金属的$F_0$是有色的(RGB三通道),而非金属的$F_0$是单通道(单色)的.

常见的$F_0$值如下: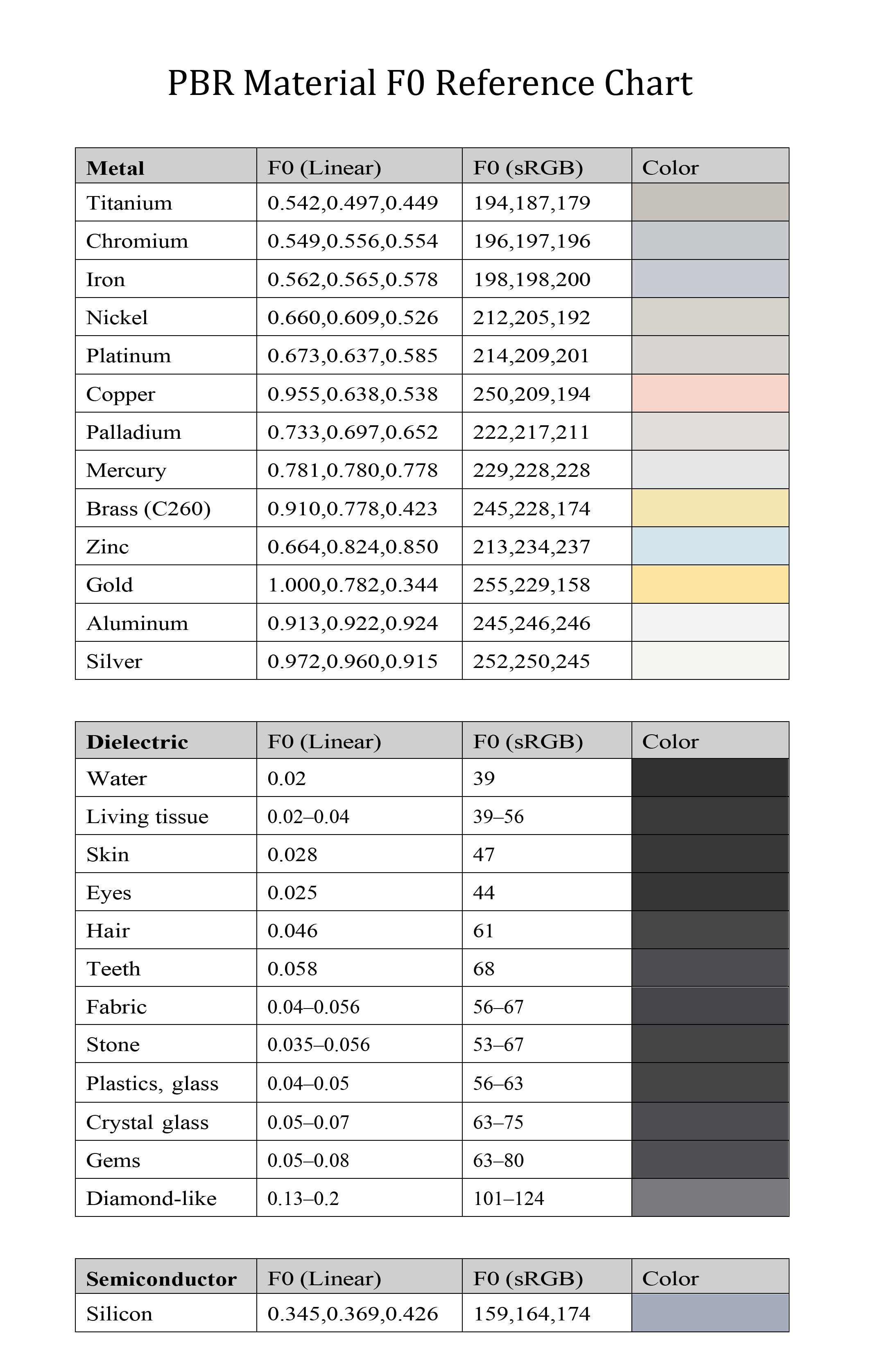

一些规律:

• 金属的$F_0$值几乎都大于0.5
• 金属的所有可见颜色都来自镜面反射(菲涅尔反射)
• 绝缘体的$F_0$值大部分都低于0.17甚至更低
• 半导体的$F_0$在[0.2,0.45]

BRDF

如前文介绍,我们可以将BRDF分为直接反射部分和漫反射部分.
漫反射部分非常好求,我们可以使用Lambertian模型.

Diffuse(Lambertian)

漫反射是指,一个光线打到表面,会被均匀地反射到各个方向.因此BRDF是一个常数$c$

由此可以有推出: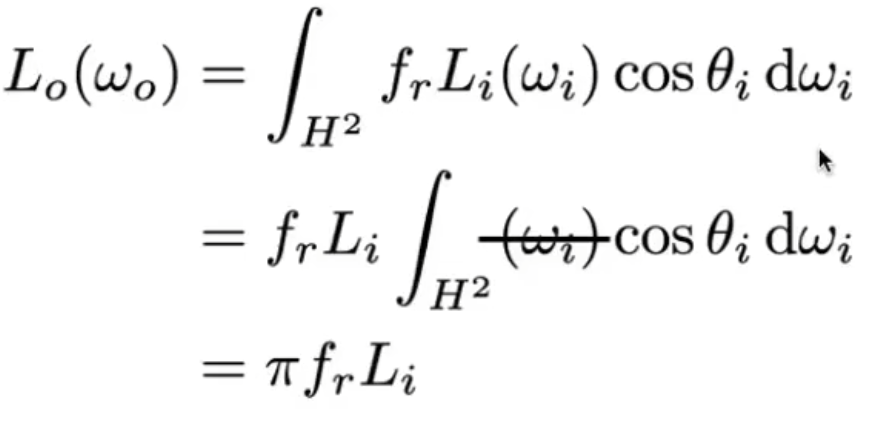

我们定义albedo(反射率),则:

$fr = albedo / pi$

---

但是到了直接反射部分时,问题就变得更加复杂了起来.在此之前,我们先看看不同材质的BRDF(直接反射部分)长什么样.

Gloosy 材质

Gloosy的BRDF大概长这样: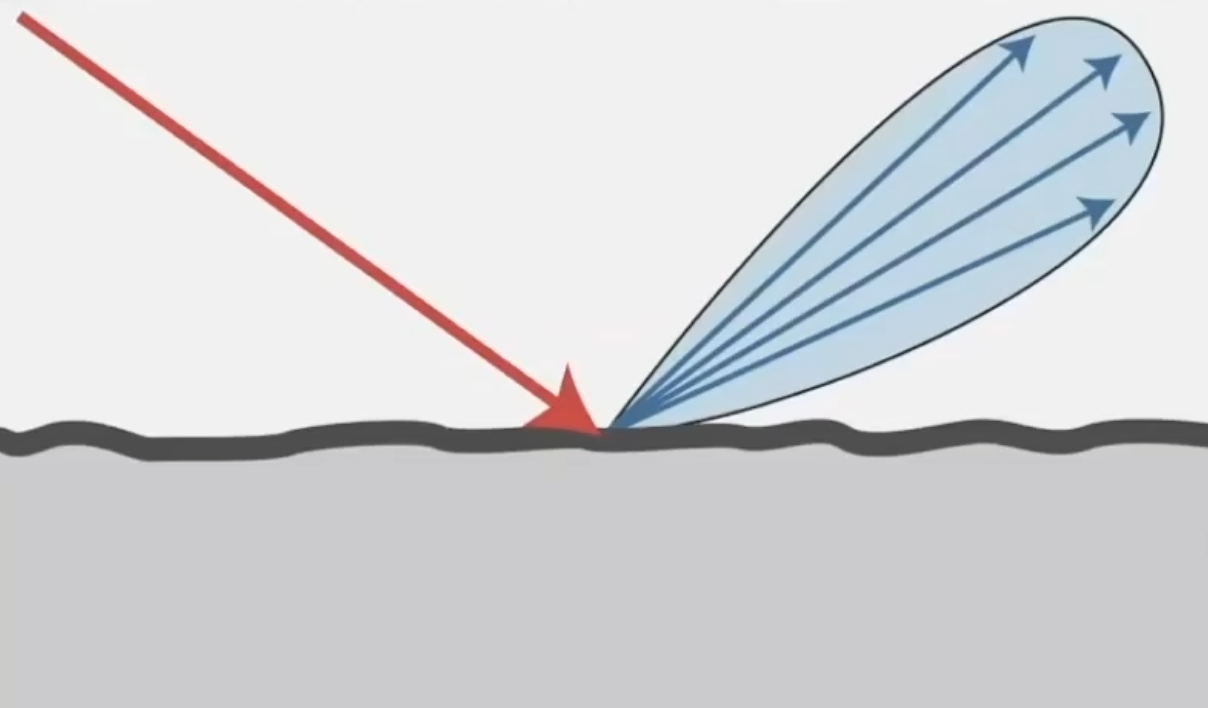

Perfect Specular Reflection 材质

镜面反射材质BRDF长这样

---

这么多种不同的BRDF,长相各不相同,我们是否有一个统一的模型可以用来描述所有材质的BRDF呢?

当然!那就是基于Microfacet Model 的 Cook Torrance模型

Microfacet Model

微表面模型的Motivation来源于太空:

当距离地球足够远时,原本的山峰沟壑都变成了平面,地球就像是一个材质球.

微平面理论是将物体表面建模成无数微观尺度上有随机朝向的理想镜面反射的小平面（microfacet）的理论。微观几何（microgeometry）的效果是在表面上的不同点处改变微平面的法线，从而改变反射和折射的光方向。出于着色的目的，通常会用统计方法处理这种微观几何现象，将表面视为具有微观结构法线的随机分布，并将宏观表面视为在每个点处多个方向上反射（和折射）光的集合。在微观尺度上，表面越粗糙，反射越模糊，表面越光滑，反射越集中

通过研究微表面的法线分布,可以对于不同的材质: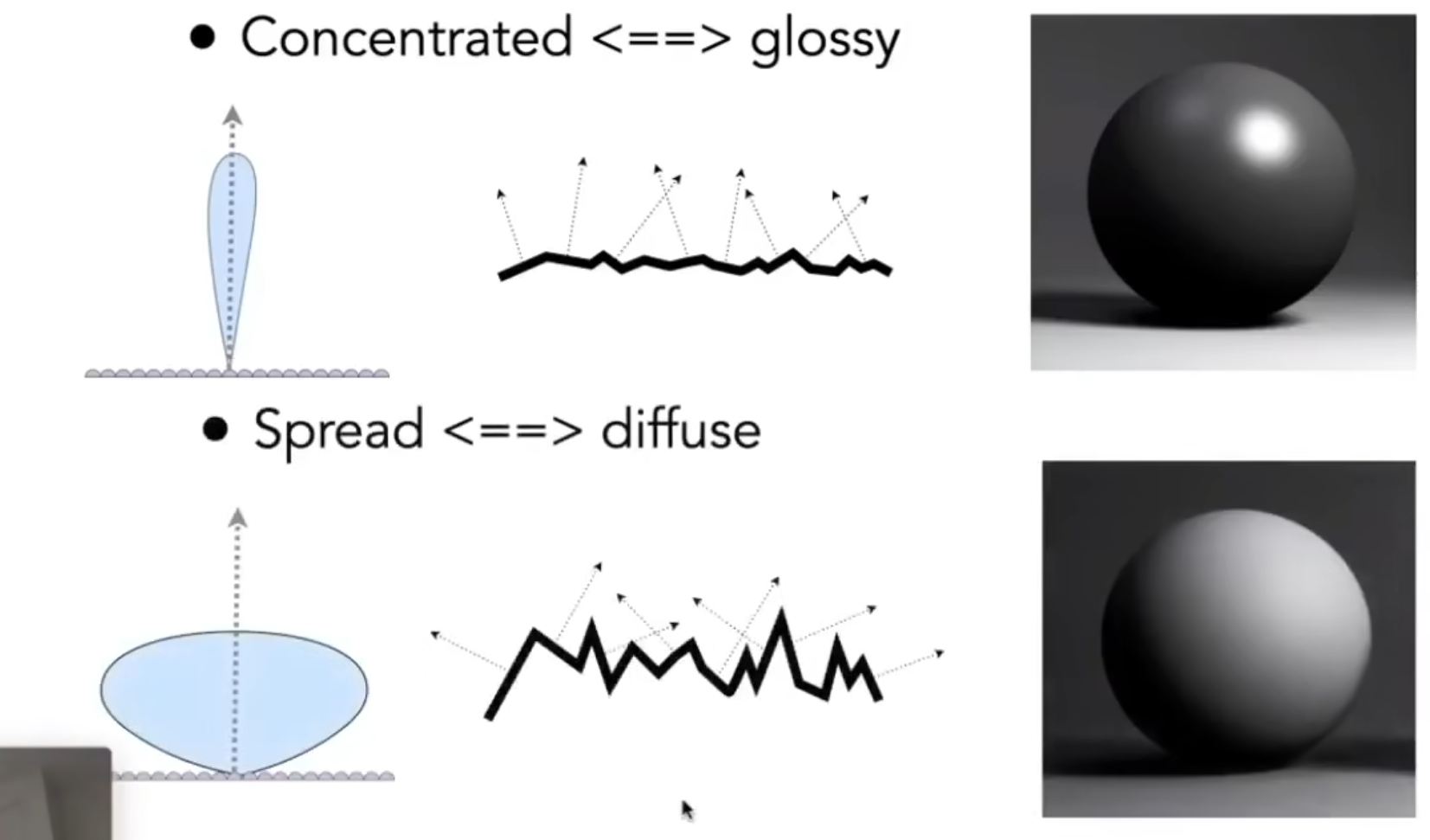

这不就统一了上文提到的三种材质吗?

那么Microfacet Model的BRDF怎么计算呢?

常用的模型是Cook-Torrance模型.

公式如下:

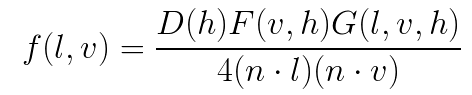
其中:

• $D(h)$ : 法线分布函数,描述正确朝向的法线的浓度.
• $F(l,h)$ : 菲涅尔函数,描述不同的表面角下表面所反射的光线所占的比率.
• $G(l,v,h)$ : 几何函数,描述微平面自成阴影的属性，即m = h的未被遮蔽的表面点的百分比.
• $分母 4(n-l)(n*v)$ : 校正因子（correctionfactor），作为微观几何的局部空间和整个宏观表面的局部空间之间变换的微平面量的校正.

tips:

• 分母中的点积,仅仅避免负值是不够的 - 也必须避免零值.通常通过在常规的clamp或绝对值操作之后添加非常小的正值来完成
• Microfacet Cook-Torrance BRDF是实践中使用最广泛的模型,实际上也是人们可以想到的最简单的微平面模型.它仅对几何光学系统中的单层微表面上的单个散射进行建模,没有考虑多次散射,分层材质,以及衍射.不过如果考虑了就是Microfacet BxDF了.

需要注意的是,$BRDF = fr_d + fr_s$, 即漫反射 + 镜面反射. 上面的公式是镜面反射部分,漫反射部分 $fr_d = albedo / pi$.

所以公式总写为:

$F(l,h) =\frac{c}{\pi} + \frac{D(h)F(l,h)G(l,v,h)}{4(n-l)(n*v)}$

那么,这些D,F,G函数具体怎么计算呢?

D(h)函数

NDF(Normal Distribution Function) D的常见模型如下:

• Beckmann [1963]
• Blinn-Phong [1977]
• GGX [2007]
• GTR [2012]
• Anisotropic Beckmann [2012]
• Anisotropic GGX [2015]

目前主流的法线分布函数是GGX,因为有更好的长尾.

GGX的公式如下:

$D(h) = \frac{\alpha^2}{(\pi (n.h)^2(\alpha^2-1)+1)}$

F 函数

菲涅尔函数常见模型如下:

• Cook-Torrance [1982]
• Schlick [1994]
• Gotanta [2014]

目前主流的菲涅尔函数是Schlick,因为成本低,精度够.

Schlick的公式如下:

$F(l,h) = F_0 + (1-F_0)(1-cos(l.h))^5$

G 函数

几何函数G的常见模型如下:

• Smith [1967]
• Cook-Torrance [1982]
• Neumann [1999]
• kelemen [2001]
• Implicit [2013]

其中,Eric Heitz在[Heitz14]中展示了Smith几何阴影函数是正确且更准确的G项,并将其拓展为Smith联合遮蔽阴影函数(Smith Joint Masking-Shadowing Function).该函数有四种形式,常用且最为简单的形式是:分离遮蔽阴影(Seperable Masking and Shadowing Function).该形式将G分为两个独立部分:光线方向,实现方向.并对两者使用相同分布函数进行描述.根据这种思想结合NDF以及Smith G,有了以下新的Smith G:

• Smith-GGX
• Smith-Beckmann
• Smith-Schlick
• Schlick-Beckmann
• Schlick-GGX

其中UE4使用的是Schlick-GGX.

Schlick-GGX的公式如下:

$k = \frac{\alpha}{2}$

$\alpha = (\frac{roughness + 1}{2})^2$

$G_1 (v) = \frac{n.v}{(n.v)(1-k)+k}$

$G(l,v,h) = G_1(l)G_1(v)$

常见PBR工作流

上文介绍了PBR的理论部分,在实际中,人们又是如何进行操作的呢?

首先列出BxDF各模型需要的参数:

BRDF:

• Roughness: 粗糙度
• F0: 菲涅尔反射系数

下文中的各个工作流只列出其中特别的贴图,其他如下文通用各类贴图不再列出.

Additional Maps:

• BumpMap
• NormalMap
• AOMap
• EmissiveMap
• HeightMap
• etc.

Metallic Workflow

BxDF类型: BRDF

---

Maps:

• AlbedoMap
  • RGB三通道
  • 存储金属镜面反射颜色
  • 存储非金属漫反射颜色
• MetalicMap
  • 灰度图(单通道)
  • 存储金属度
• RoughnessMap
  • 灰度图(单通道)
  • 存储粗糙度

---

Metallic工作流没有使用$F_0$,而是使用了金属度的概念.

$F_0$的计算方法如下:

vec3 F0 = vec3(0.04); 
F0 = mix(F0, albedo, metallic);

PBR金属流假设了所有绝缘体的F0 = 0.04.
然后使用金属度数据来混合F0和albedo.因为albedo存储了金属的反射颜色.

---

Pros & Cons:

• 非金属F0固定为0.04无法调整
• 主流的工作流
• 金属度更易理解

---

Metallic Workflow Shader实现示例:

#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
in vec3 WorldPos;
in vec3 Normal;

// material parameters
uniform sampler2D albedoMap;
uniform sampler2D normalMap;
uniform sampler2D metallicMap;
uniform sampler2D roughnessMap;
uniform sampler2D aoMap;

// lights
uniform vec3 lightPositions[4];
uniform vec3 lightColors[4];

uniform vec3 camPos;

const float PI = 3.14159265359;

float DistributionGGX(vec3 N, vec3 H, float roughness);
float GeometrySchlickGGX(float NdotV, float roughness);
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness);
vec3 fresnelSchlickRoughness(float cosTheta, vec3 F0, float roughness);

void main()
{   
    vec3 albedo     = pow(texture(albedoMap, TexCoords).rgb, 2.2);
    vec3 normal     = getNormalFromNormalMap();
    float metallic  = texture(metallicMap, TexCoords).r;
    float roughness = texture(roughnessMap, TexCoords).r;
    float ao        = texture(aoMap, TexCoords).r;

    vec3 N = normalize(Normal);
    vec3 V = normalize(camPos - WorldPos);

    vec3 F0 = vec3(0.04); 
    F0 = mix(F0, albedo, metallic);

    // reflectance equation
    vec3 Lo = vec3(0.0);
    for(int i = 0; i < 4; ++i) 
    {
        // calculate per-light radiance
        vec3 L = normalize(lightPositions[i] - WorldPos);
        vec3 H = normalize(V + L);
        float distance    = length(lightPositions[i] - WorldPos);
        float attenuation = 1.0 / (distance * distance);
        vec3 radiance     = lightColors[i] * attenuation;        

        // cook-torrance brdf
        float NDF = DistributionGGX(N, H, roughness);        
        float G   = GeometrySmith(N, V, L, roughness);      
        vec3 F    = fresnelSchlick(max(dot(H, V), 0.0), F0);       

        vec3 kS = F;
        vec3 kD = vec3(1.0) - kS;
        kD *= 1.0 - metallic;     

        vec3 nominator    = NDF * G * F;
        float denominator = 4.0 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0) + 0.001; 
        vec3 specular     = nominator / denominator;

        // add to outgoing radiance Lo
        float NdotL = max(dot(N, L), 0.0);                
        Lo += (kD * albedo / PI + specular) * radiance * NdotL; 
    }   

    vec3 ambient = vec3(0.03) * albedo * ao;
    vec3 color = ambient + Lo;

    color = color / (color + vec3(1.0));
    color = pow(color, vec3(1.0/2.2));  

    FragColor = vec4(color, 1.0);
}  

Specular Workflow

BxDF类型: BRDF

Maps:

• DiffuseMap
  • RGB三通道
  • 存储非金属漫反射颜色
  • 如果是金属则是纯黑
• SpecularMap
  • RGB三通道
  • 存储F0
• GlossnessMap
  • 灰度图(单通道)
  • 存储光滑度

---

Specular Workflow没有直接使用roughness,而是使用了glossness.

glossness的计算方法如下:

float glossiness = 1.0 - roughness;

---

pros & cons:

• 自由调整F0
  • 赋予自由度
  • 容易做出反物理材质(能量不守恒)
• 7个通道,比Metallic(5个通道)更费

---

Specular Workflow Shader实现示例:

#version 330 core

out vec4 FragColor;
in vec2 TexCoords;
in vec3 WorldPos;
in vec3 Normal;

// material parameters
uniform sampler2D albedoMap;
uniform sampler2D normalMap;
uniform sampler2D metallicMap;
uniform sampler2D roughnessMap;
uniform sampler2D aoMap;

// lights
uniform vec3 lightPositions[4];
uniform vec3 lightColors[4];

uniform vec3 camPos;

const float PI = 3.14159265359;

float DistributionGGX(vec3 N, vec3 H, float roughness);
float GeometrySchlickGGX(float NdotV, float roughness);
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness);
vec3 fresnelSchlickRoughness(float cosTheta, vec3 F0, float roughness);

void main()
{   
    vec3 albedo     = pow(texture(albedoMap, TexCoords).rgb, 2.2);
    vec3 normal     = getNormalFromNormalMap();
    float metallic  = texture(metallicMap, TexCoords).r;
    float roughness = texture(roughnessMap, TexCoords).r;
    float ao        = texture(aoMap, TexCoords).r;

    vec3 N = normalize(normal);
    vec3 V = normalize(camPos - WorldPos);

    vec3 F0 = vec3(0.04); 
    F0 = mix(F0, albedo, metallic);

    // reflectance equation
    vec3 Lo = vec3(0.0);
    for(int i = 0; i < 4; ++i) 
    {
        // calculate per-light radiance
        vec3 L = normalize(lightPositions[i] - WorldPos);
        vec3 H = normalize(V + L);
        float distance    = length(lightPositions[i] - WorldPos);
        float attenuation = 1.0 / (distance * distance);
        vec3 radiance     = lightColors[i] * attenuation;        

        // cook-torrance brdf
        float NDF = DistributionGGX(N, H, roughness);        
        float G   = GeometrySmith(N, V, L, roughness);      
        vec3 F    = fresnelSchlick(max(dot(H, V), 0.0), F0);       

        vec3 kS = F;
        vec3 kD = vec3(1.0) - kS;
        kD *= 1.0 - metallic;     

        vec3 nominator    = NDF * G * F;
        float denominator = 4.0 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0) + 0.001; 
        vec3 specular     = nominator / denominator;

        // add to outgoing radiance Lo
        float NdotL = max(dot(N, L), 0.0);                
        Lo += (kD * albedo / PI + specular) * radiance * NdotL; 
    }   

    vec3 ambient = vec3(0.03) * albedo * ao;
    vec3 color = ambient + Lo;

    color = color / (color + vec3(1.0));
    color = pow(color, vec3(1.0/2.2));  

    FragColor = vec4(color, 1.0);
}

Unity Metallic Workflow

Unity Specular Workflow

Unreal Metallic Workflow

Unreal Specular Workflow

---

Reference

• Physically Based Rendering: From Theory to Implementation
• GAMES 202
• GAMES 101
• GAMES 104
• PBR White Paper