从PCF到MSM
在实时渲染中, 有一个常常被使用的约等式: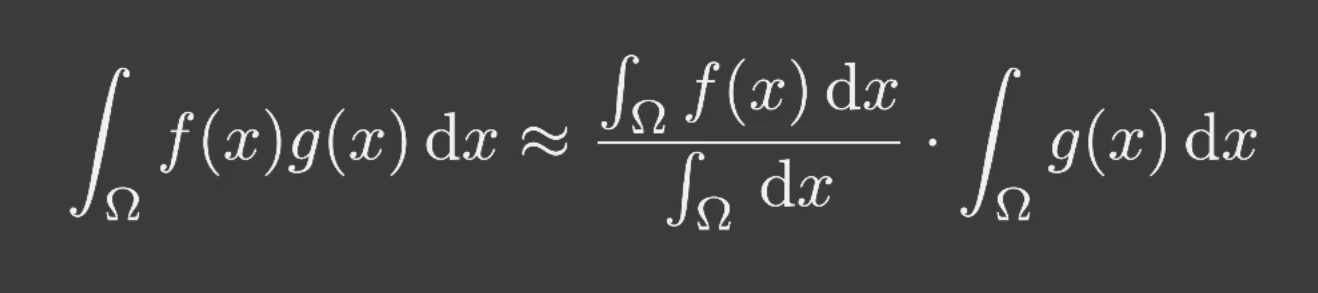
问题在于,什么时候这个等式比较正确呢?
- 积分域比较小时
- g(x)在积分域中变化不大时
在实时渲染中,对Rendering Equation有另一种解释: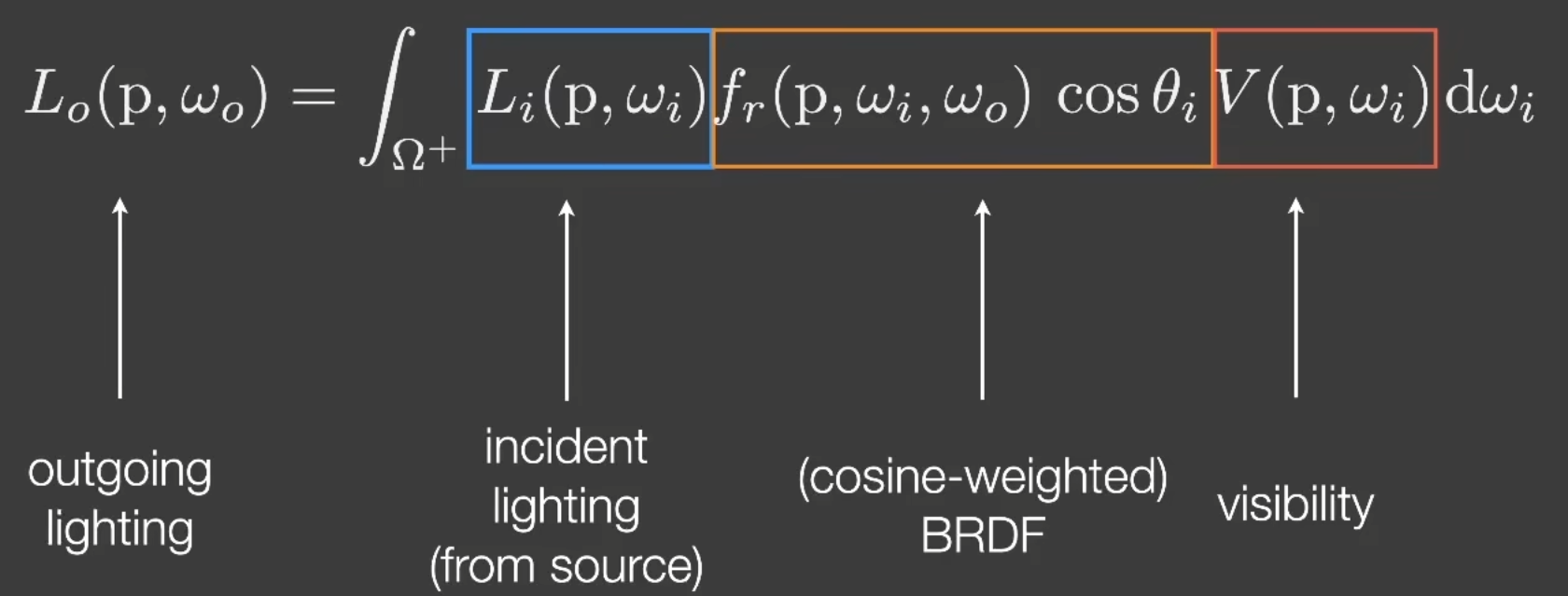
多了一项V(p,wi),表示着色点到光源的Visibility.
那么我们就可以更改Rendering Equation为:
在RTR中,由于光源大部分是点光源或方向光,使得积分域小.而brdf是diffuse的时候变化也不大.这时近似就比较准确.
总结来说:
- 点光源,方向光
- diffuse brdf/constant radiance area light
PCF(Percentage Closer Filtering)
PCF是用于解决shadowmap的锯齿问题的一种方法.
PCF的步骤如下:
- 对于每个着色像素
- 获取周围n*n个像素的深度值
- 用每个深度值与shadowmap的深度值进行比较得到一堆1和0
- 对所有1,0取平均值得到Visibility
效果如下:
注意:
- 不是对ShadowMap进行模糊
问题在于: 这开销肉眼的变大了不少,肯定会很慢.
人们发现,PCF的产生的效果不久很像软阴影了吗?而且n越大越软.
那么我们是不是将n调很大就可以实现软阴影了呢/
在此之前,一个关键的发现在于: 离遮挡物距离越近,阴影越硬.
所以filter size应该和blocker distance 相关: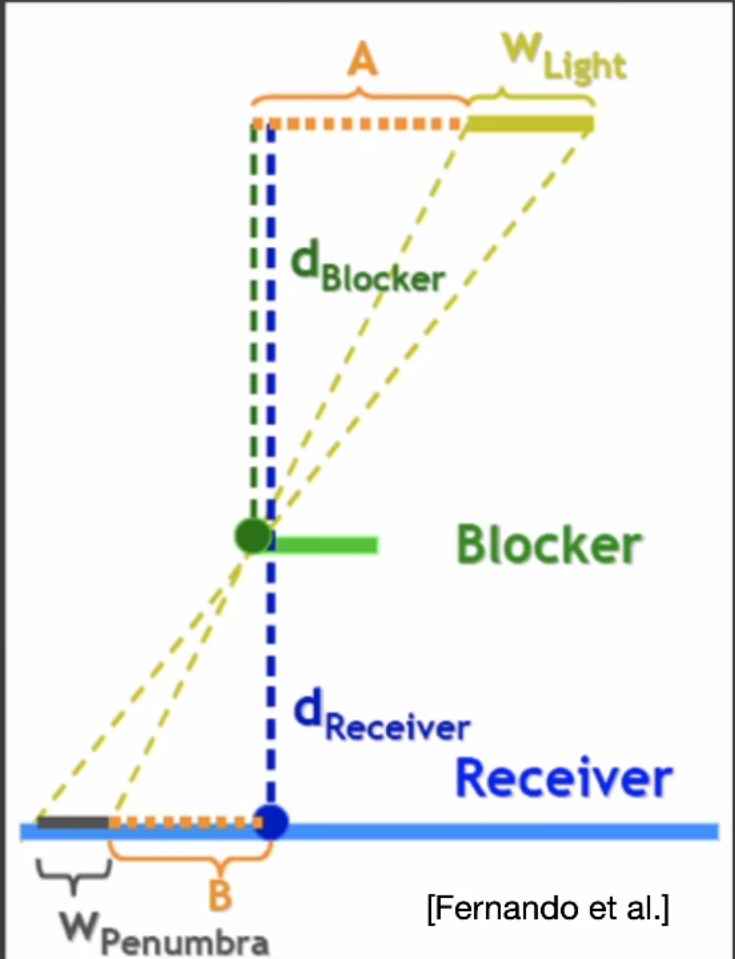
公式如下: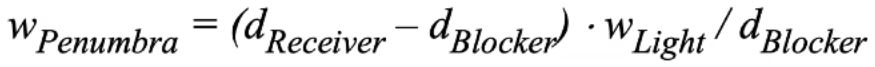
我们也可以用公式来表示PCSS: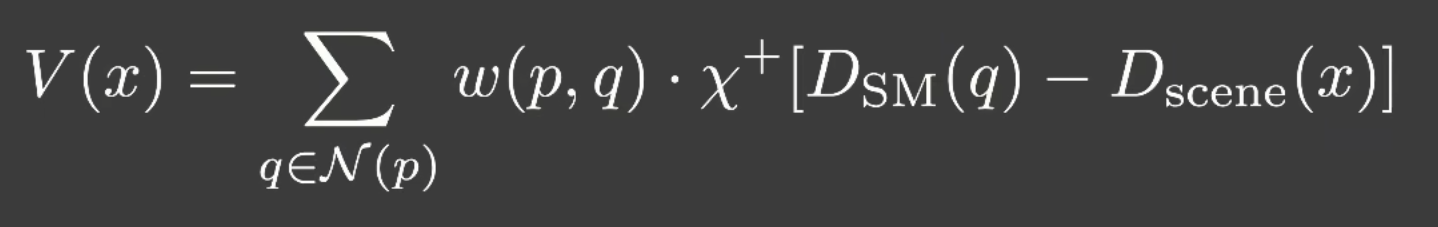
对p点邻域范围内加权平均作为visibility.
至此PCSS的前置任务已经完成.
PCSS的步骤如下:
- Blocker search: 在一定区域内计算Blocker平均深度
- Penumbra Estimation: 计算Filter Size
- PCF
问题在于如何计算用于计算Blocker区域的大小呢?
可以使用光源摄像机的近平面来确定大小.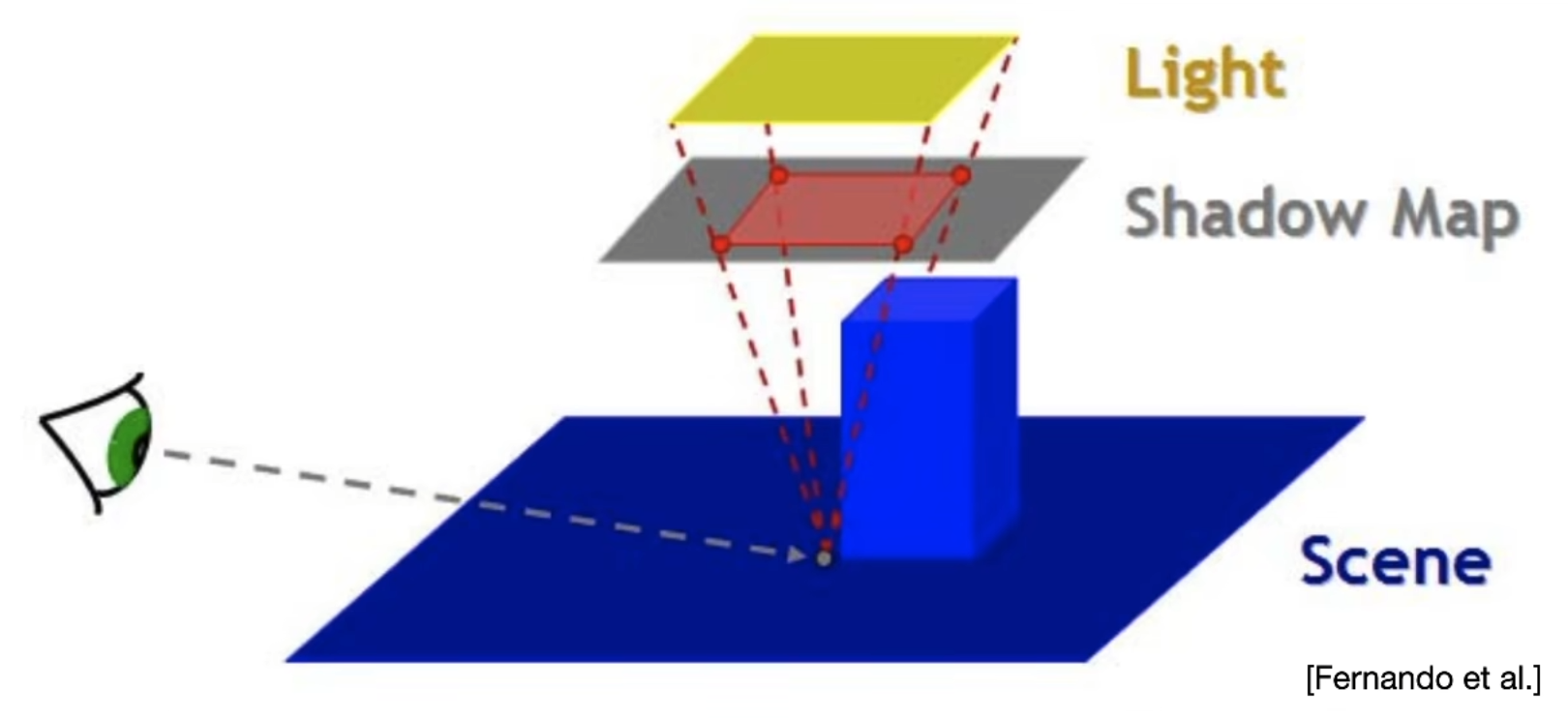
但是,这个开销肉眼可见的巨大.
其中,第1,3步的花销很大.
为了解决这个问题,人们提出了一种新方法:Variance Soft Shadow Mapping(VSSM).
VSSM关键就在于加速了PCF计算.
为了理解VSSM,我们首先要回顾PCF–PCF计算了有多少深度要小于自己.
我们可以通过概率论取近似这个值.更极端一点,我们可以认为这个分布就是一个正态分布.
一个正态分布的需要两个数据:均值和方差.
对于均值我们可以使用:
- mipmap
不准(分辨率太低),只能方形 - SAT(Sumed Area Table)
计算方差,我们使用这个公式: var(x) = e(x^2) - [e(x)]^2.
对于后面一项我们直接平方,对于前面一项,我们需要一张额外的shadowmap记录深度的平方.这张额外的shadowmap可以在生成shadowmap的同时顺带生成.
好了,我们现在计算出了我们需要的正态分布,我们如何计算曲线下的面积(多少深度满足要求)呢?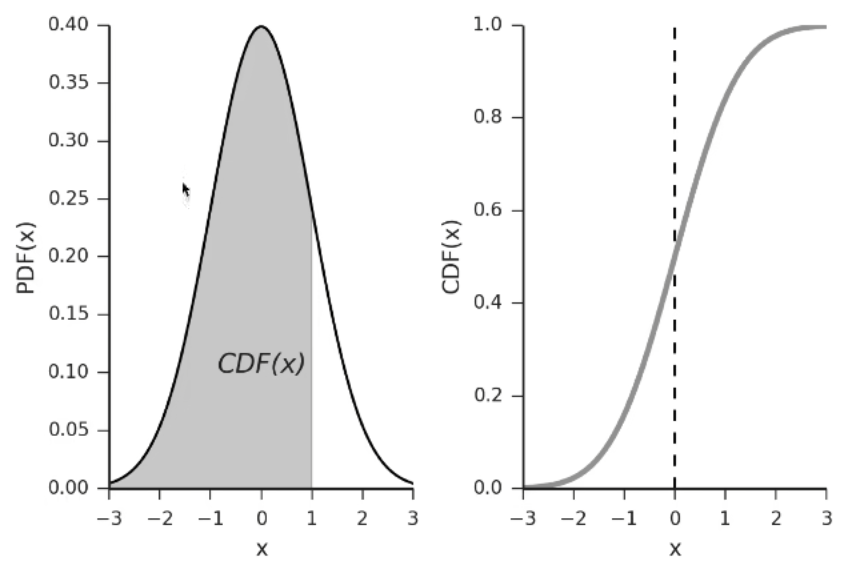
那么如何去算这个面积呢?
使用error function来计算(实际上没有解析解,只有数值解).
然而计算error function的开销很大,所以VSSM又拿出了一个神奇的东西:切比雪夫不等式.
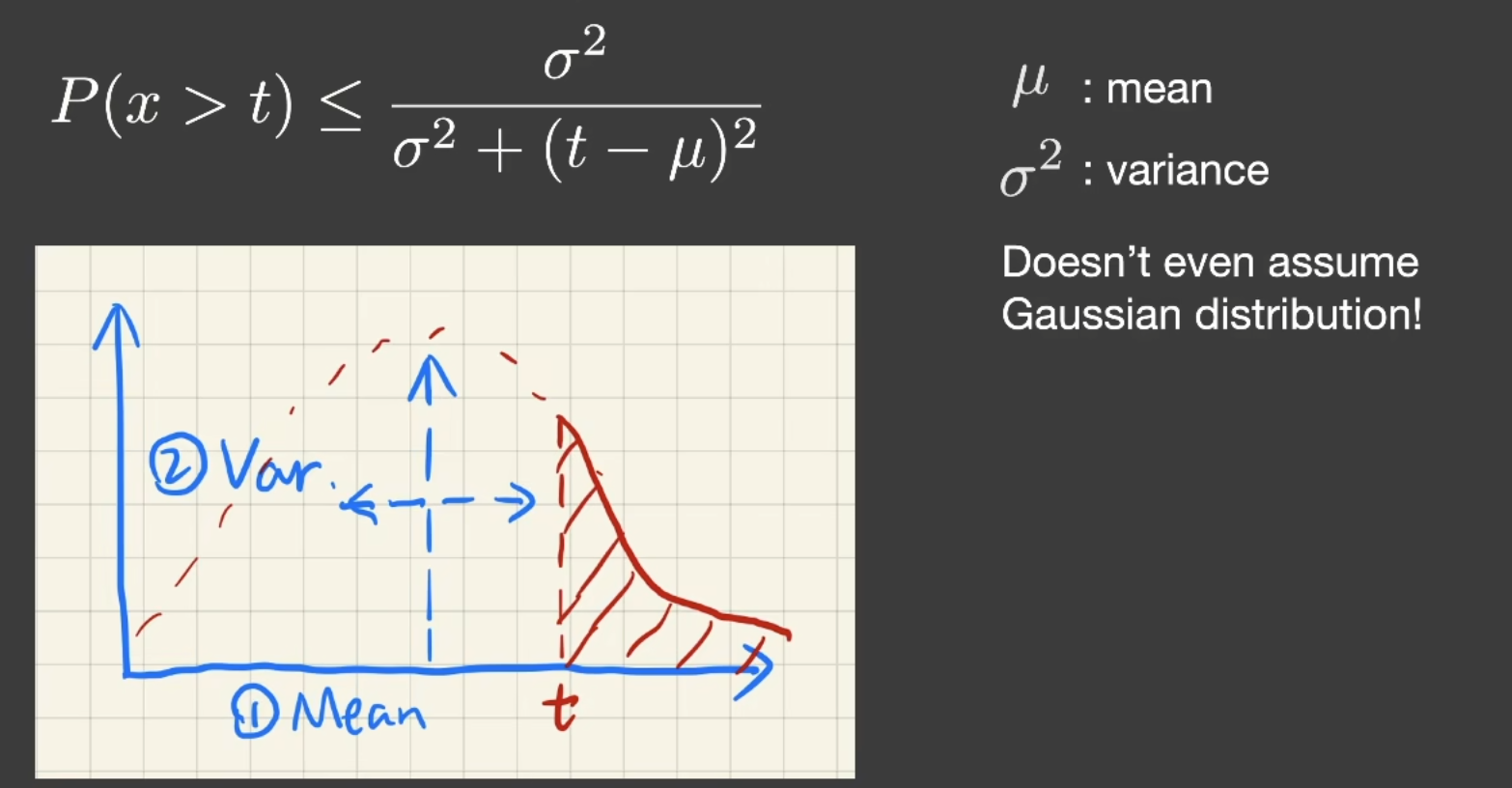
看了上文,读者可能会想起:图形学没有不等式,只有约等式.
所以我们改写为切比雪夫约等式.
好消息是,切比雪夫不等式不在乎是否是正态分布,所以前面我们假设分布是正态分布的假设可以取消了.
VSSM流程如下:
shadow map generation: 计算深度平方,生成shadow map
RunTime:
- 获取深度平均值:O(1)
- 获取深度平方:O(1)
- 切比雪夫计算Visibility:O(1)
这样,就消去了Sample和loop而只增加了一点生产mipmap的开销,从而大大加速了第三步.
但是第一步如何加速呢?
我们再回看一下第一步计算了什么:一定区域内遮挡物的平均深度(图中蓝色区域平均深度)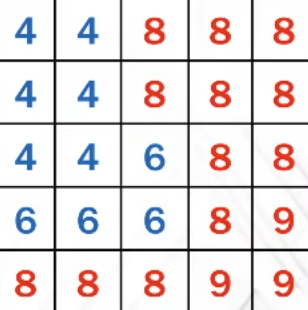
不难发现有以下关系: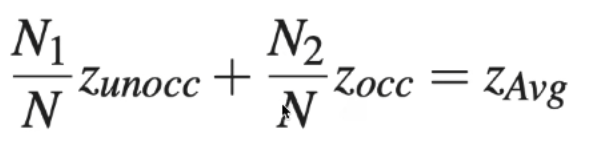
前面的因子是否有点让人熟悉–不就是占比吗?那不是又可以切比雪夫了吗?
那么我们就就可以计算出两个系数,但我们还需要知道Zunocc才可以计算Zocc.
VSSM计算方法是: 假设Zunocc = t.
好了,解决了.
回顾一下VSSM做了哪些假设:
- 切比雪夫约等式
- Zunocc = t
现在回到VSSM第一个问题,给与一个区域,如何快速得到这个区域的均值?
第一个想法肯定是MipMap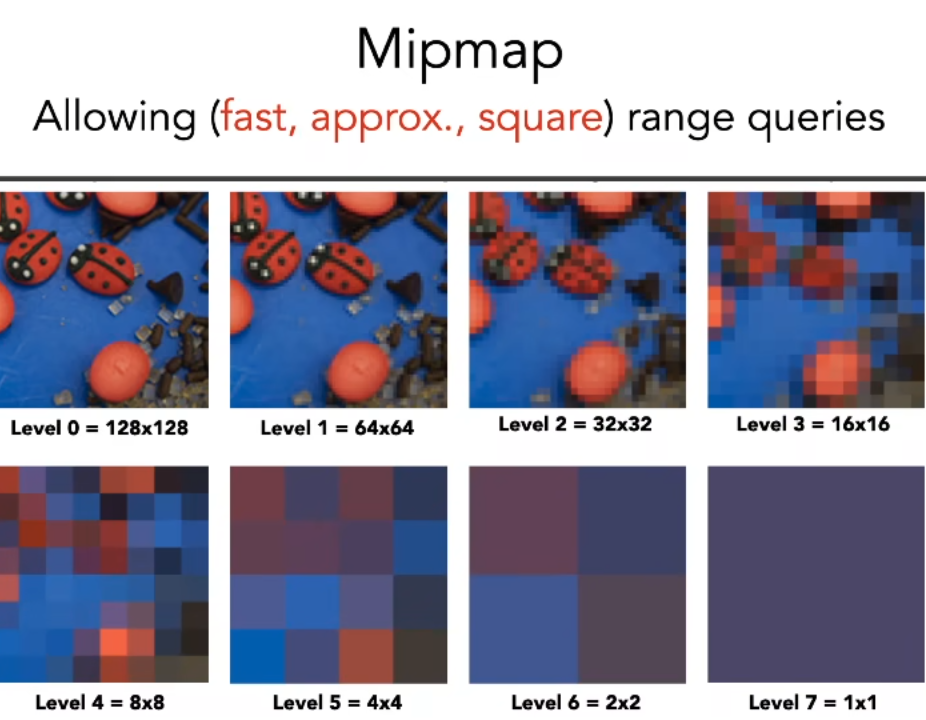
但是MipMap不是很准,有以下原因:
- 采样点如果离mipmap像素中心较远,双线性插值结果不准
- 如果范围不是2的平方,三线性插值更不准
结论:mipmap用来做范围查询不准.
那么用什么数据结构才准呢?答案是SAT(Sumed Area Table).
SAT实际上就是前缀和,输入两个点,用后面的点减去前面的点然后除以N就可以得到绝对准确的均值.
下面详细解释一下,先看一维情况: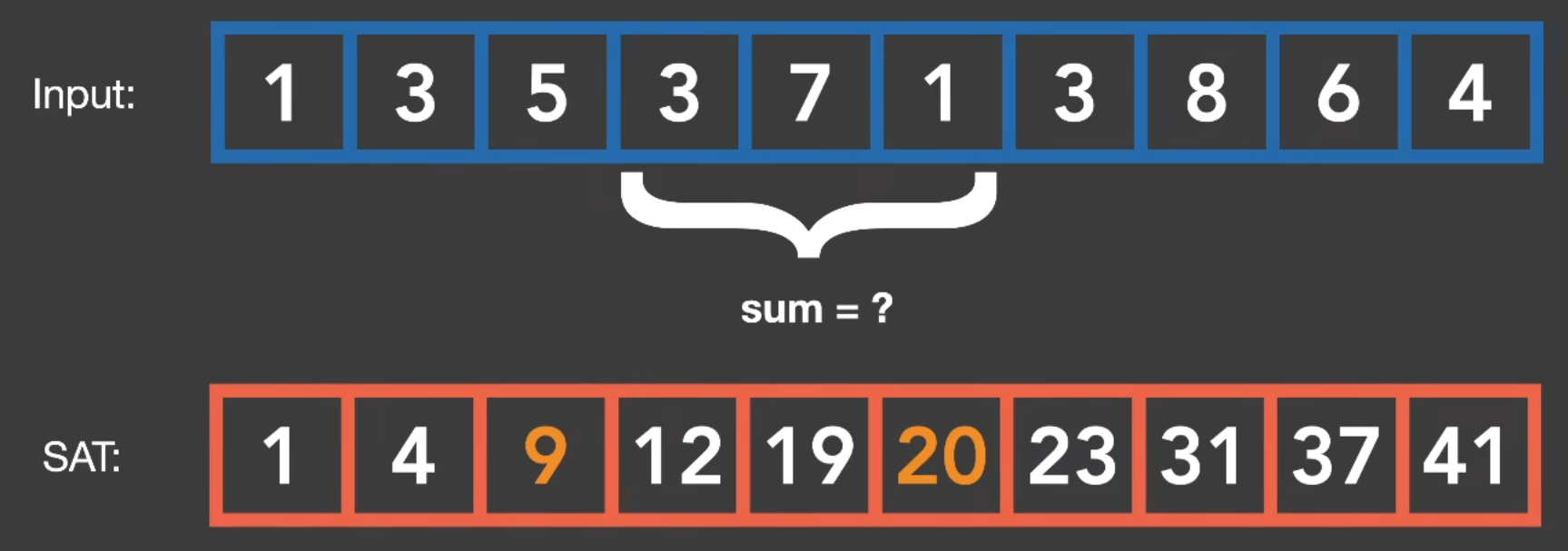
对于二维情况:
在这个图中,sat[y][x]表示从左上角加到(x,y)的值.
SAT好消息是比较准确(数值累加积累误差),但是build需要O(n)时间和O(n)存储.
Moment shadow mapping
VSSM这么多假设,没有问题吗?当然有!主要就是当模拟的分布和实际分布差距很大时,就会出现问题.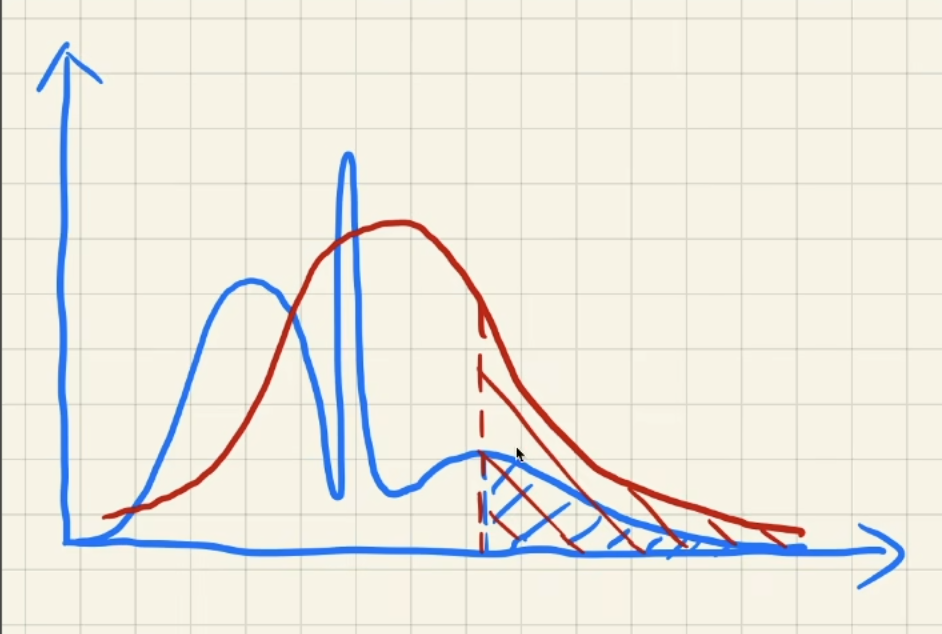
当如果估计的结果比实际黑时可能还能接受,但变白的话就会让人很暗接受–也就是light leaking问题.

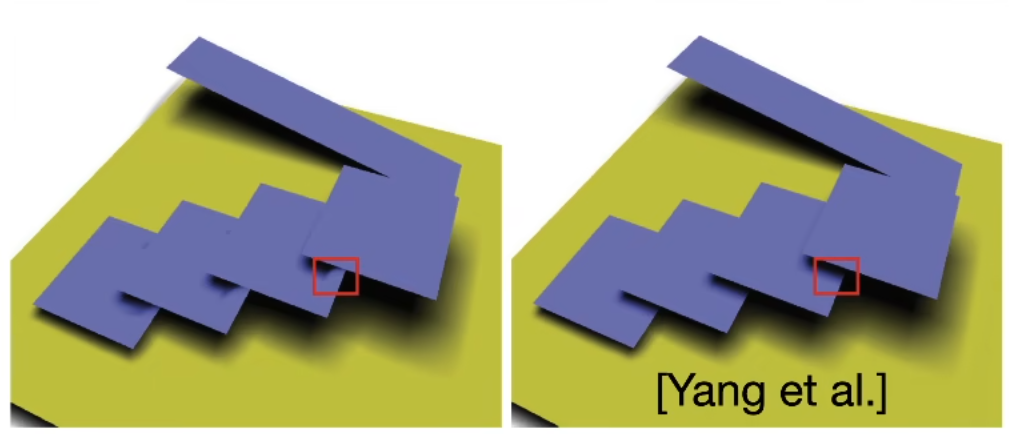
问题核心在于VSSM描述分布不准确,而Moment Shadow Mapping就是来解决这个问题的.
想要描述更准确,当然需要增加新的参数.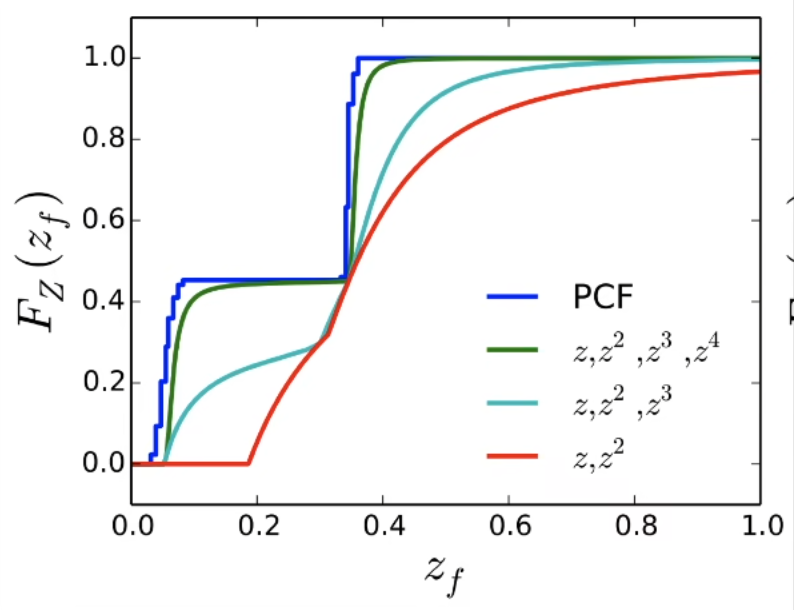
VSSM 存储了x,x^2.
而增加新的x^3,x^4就是MSM的思想.
但是问题是,给你前四阶矩,如何计算呢?看论文去吧,有点复杂.


